Question

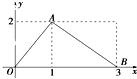函数f（x）的图象是如下图所示的折线段OAB，点A的坐标为（1，2），点B的坐标为（3，0）
（1）f（x）的解析式；
（2）定义函数g（x）=f（x）•（x-1），求函数g（x）的最大值．

Answer 1

考点：函数解析式的求解及常用方法

专题：函数的性质及应用

分析：（1）根据图象判断为一次式，求斜率，用点斜式求解，分段表示．
（2）分段求解最大值，最后确定整个函数的最大值．

解答： 解：（1）∵折线段OAB，点A的坐标为（1，2），点B的坐标为（3，0），
∴k_OA=2，k_AB=-1，
可得OA：y=2x，0＜x＜1
AB：y=-x+3，1＜x＜3
∴f（x）=

2x，0＜x＜1 -x+3，1＜x＜3

（2）定义函数g（x）=f（x）•（x-1），
函数g（x）=

2x(x-1)，0＜x＜1 (3-x)(x-1)，1＜x＜3

，
当0＜x＜1时最大值为-

1

2

，
当1＜x＜3时最大值为1，
函数g（x）的最大值为1

点评：本题考查了分段函数解析式的求解，最大值的求解，注意计算准确即可，难度不大．