题目内容

i+i2+i3+i4=
 
．
考点：虚数单位i及其性质
专题：数系的扩充和复数
分析：直接利用虚数单位i的运算性质化简求值．
解答： 解：i+i2+i3+i4=i-1+i2•i+i2•i2=i-1-i+1=0．
故答案为：0．
点评：本题考查了虚数单位i的运算性质，是基础的会考题型．
练习册系列答案
相关题目
“直线y=kx+2与圆x2+y2=1相切”是“k=
3
”的（　　）
A、充分不必要条件
B、必要不充分条件
C、充要条件
D、既不充分也不必要条件
已知两定点M（-2，0），N（2，0），若直线上存在点P，使得|PM|-|PN|=2，则称该直线为“A型直线”．给出下列直线：①y=x+1，②y=
3
x+2，③y=-x+3，④y=-2x．
其中是“A型直线”的序号是
 
．
已知二项式（ax+
1
x
）3展开式中各项的系数和为64，则a=
 
．
已知等差数列{an}的前n项和为Sn，若a3+a17=10，则S19=
 
．
函数f（x）为偶函数，且x∈（-∞，0）时，f（x）=x（x-1），则x∈（0，+∞）时，f（x）为（　　）
A、x（x+1）
B、-x（-x+1）
C、x（-x+1）
D、x（x-1）
已知直线（3a+2）x+（1-4a）y+8=0与（5a-2）x+（a+4）y-7=0垂直，则a的值为（　　）
A、0或1B、1C、0D、-1
计算：
（1）8
2
3
-
(
2
-1)2
+2log23+(
1
3
)0
（2）（lg5）2+lg2•lg50．
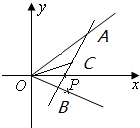如图所示，射线OA、OB分别与x轴正半轴成45°和30°角，过点P（1，0）作直线AB分别交OA、OB于A、B两点，当AB的中点C恰好落在直线y=
1
2
x上时，求直线AB的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网