题目内容
已知定义在区间[0,2]上的两个函数f(x)和g(x),其中f(x)=-x2+2ax+1+a2,g(x)=x-
+
,
(Ⅰ)求函数f(x)的最小值;
(Ⅱ)对于?x1,x2∈[0,2],f(x1)>g(x2)恒成立,求实数a的取值范围.
| 1 |
| 4 |
| 2-x |
(Ⅰ)求函数f(x)的最小值;
(Ⅱ)对于?x1,x2∈[0,2],f(x1)>g(x2)恒成立,求实数a的取值范围.
考点:函数恒成立问题
专题:函数的性质及应用
分析:(Ⅰ)根据二次函数的图象和性质,即可求函数f(x)的最小值;
(Ⅱ)对于?x1,x2∈[0,2],f(x1)>g(x2)恒成立,转化为求两个函数是最值即可求实数a的取值范围.
(Ⅱ)对于?x1,x2∈[0,2],f(x1)>g(x2)恒成立,转化为求两个函数是最值即可求实数a的取值范围.
解答:
解:(Ⅰ)∵f(x)=-x2+2ax+1+a2,
∴函数的对称轴为x=a,则区间[0,2]的中点为x=1,
当a≤1时,函数f(x)的最小值为f(2)=a2+4a-3;
当a>1时,函数f(x)的最小值为f(0)=1+a2;
综上函数f(x)的最小值为f(x)min=
.
(Ⅱ)设t=
,则0≤t≤
,
则x=2-t2,
∴g(x)=m(t)=-t2+t+
,
则对称轴为t=
,
∴g(x)max=2,
要使f(x1)>g(x2)恒成立,只要f(x)min>g(x)max即可,
∴当a≤1时,f(x)min=a2+4a-3>2,
解得:a<-5,
当a>1时,f(x)min=1+a2>2
解得:a>1,
综上所述,a∈(-∞,-5)∪(1,+∞).
∴函数的对称轴为x=a,则区间[0,2]的中点为x=1,
当a≤1时,函数f(x)的最小值为f(2)=a2+4a-3;
当a>1时,函数f(x)的最小值为f(0)=1+a2;
综上函数f(x)的最小值为f(x)min=
|
(Ⅱ)设t=
| 2-x |
| 2 |
则x=2-t2,
∴g(x)=m(t)=-t2+t+
| 7 |
| 4 |
则对称轴为t=
| 1 |
| 2 |
∴g(x)max=2,
要使f(x1)>g(x2)恒成立,只要f(x)min>g(x)max即可,
∴当a≤1时,f(x)min=a2+4a-3>2,
解得:a<-5,
当a>1时,f(x)min=1+a2>2
解得:a>1,
综上所述,a∈(-∞,-5)∪(1,+∞).
点评:本题主要考查函数恒成立问题,利用换元法将函数转化为二次函数是解决本题的关键,考查学生的计算能力.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
以下判断正确的是( )
| A、函数y=f(x)为R上的可导函数,则f′(x0)=0是x0为函数f(x)极值点的充要条件 |
| B、命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1>0” |
| C、命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为假命题 |
| D、“b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件 |
 如图是一个从A→B的”闯关”游戏.规则规定:每过一关前都要抛掷一个在各面上分别标有1,2,3,4的均匀的正四面体.在过第n(n=1,2,3)关时,需要抛掷n次正四面体,如果这n次面朝下的数字之和大于2n,则闯关成功.
如图是一个从A→B的”闯关”游戏.规则规定:每过一关前都要抛掷一个在各面上分别标有1,2,3,4的均匀的正四面体.在过第n(n=1,2,3)关时,需要抛掷n次正四面体,如果这n次面朝下的数字之和大于2n,则闯关成功.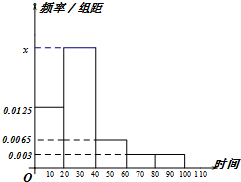 某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].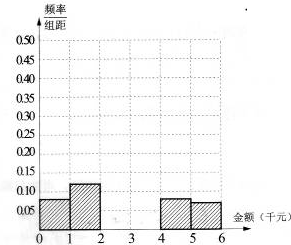 某网络营销部门随机抽查了某市200名网友在2013年11月11日的网购金额,所得数据如下表:
某网络营销部门随机抽查了某市200名网友在2013年11月11日的网购金额,所得数据如下表: