题目内容
某次数学测验共有10道选择题,每道题共有四个选项,且其中只有一个选项是正确的,评分标准规定:每选对1道题得5分,不选或选错得0分.某考生每道题都选并能确定其中有6道题能选对,其余4道题无法确定正确选项,但这4道题中有2道题能排除两个错误选项,另2道只能排除一个错误选项,于是该生做这4道题时每道题都从不能排除的选项中随机选一个选项作答,且各题作答互不影响.
(Ⅰ)求该考生本次测验选择题得50分的概率;
(Ⅱ)求该考生本次测验选择题所得分数的分布列和数学期望.
(Ⅰ)求该考生本次测验选择题得50分的概率;
(Ⅱ)求该考生本次测验选择题所得分数的分布列和数学期望.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)设选对一道“能排除2个选项的题目”为事件A,选对一道“能排除1个选项的题目”为事件B,该考生选择题得50分的概率为P(A)P(A)P(B)P(B),由此能求出结果.
(Ⅱ)该考生所得分数X=30,35,40,45,50,分别求出P(X=30),P(X=35),P(X=40),P(X=45),P(X=50),由此能求出X的分布列和数学期望.
(Ⅱ)该考生所得分数X=30,35,40,45,50,分别求出P(X=30),P(X=35),P(X=40),P(X=45),P(X=50),由此能求出X的分布列和数学期望.
解答:
解:(Ⅰ)设选对一道“能排除2个选项的题目”为事件A,
选对一道“能排除1个选项的题目”为事件B,
则P(A)=
,P(B)=
,
该考生选择题得50分的概率为:
P(A)P(A)P(B)P(B)=(
)2•(
)2=
.
(Ⅱ)该考生所得分数X=30,35,40,45,50,
P(X=30)=(
)2(1-
)2=
,
P(X=35)=
(
)2(
)2+(
)2•
•
•
=
,
P(X=40)=(
)2(
)2+
(
)2
•
•
+(
)2(
)2=
,
P(X=45)=
(
)2(
)2+(
)2
•
•
=
,
P(X=50)=(
)2(
)2=
,
∴X的分布列为:
EX=30×
+35×
+40×
+45×
+50×
=
.
选对一道“能排除1个选项的题目”为事件B,
则P(A)=
| 1 |
| 2 |
| 1 |
| 3 |
该考生选择题得50分的概率为:
P(A)P(A)P(B)P(B)=(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 36 |
(Ⅱ)该考生所得分数X=30,35,40,45,50,
P(X=30)=(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 9 |
P(X=35)=
| C | 1 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| C | 1 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
P(X=40)=(
| 1 |
| 2 |
| 2 |
| 3 |
| C | 1 2 |
| 1 |
| 2 |
| C | 1 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 13 |
| 36 |
P(X=45)=
| C | 1 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| C | 1 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 6 |
P(X=50)=(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 36 |
∴X的分布列为:
| X | 30 | 35 | 40 | 45 | 50 | ||||||||||
| P |
|
|
|
|
|
| 1 |
| 9 |
| 1 |
| 3 |
| 13 |
| 36 |
| 1 |
| 6 |
| 1 |
| 36 |
| 115 |
| 3 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望,是中档题,在历年的高考中都是必考题型.

练习册系列答案
相关题目
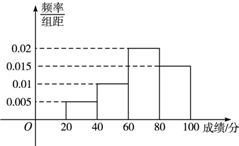 某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100],则该次英语测试该班的平均成绩是( )
某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100],则该次英语测试该班的平均成绩是( )| A、63 | B、65 | C、68 | D、70 |
 为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十进制)如图所示,假设得分值的中位数为a,众数为b,平均值为c,则( )
为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十进制)如图所示,假设得分值的中位数为a,众数为b,平均值为c,则( )| A、a=b=c |
| B、a<c<b |
| C、a<b<c |
| D、b<a<c |
 如图所示的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=2AB,CE与平面ACD所成角为45°,F、H分别为CD、DE中点.
如图所示的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=2AB,CE与平面ACD所成角为45°,F、H分别为CD、DE中点.