题目内容
已知集合A={x|2x2-x-3=0},B={x|ax+2=0},若A∩B=B,求实数a的值.
考点:集合的包含关系判断及应用
专题:集合
分析:首先,化简集合A,然后结合A∩B=B,得到B⊆A,分为B=∅和B≠∅两种情形进行讨论.
解答:
解:由集合A得:A={-1,
},
当B=∅时,
此时a=0,满足条件;
当B≠∅时,即a≠0,
∴B={-
}
∵A∩B=B,∴B⊆A
∴-
=-1或-
=
,
解得a=2或a=-
,
∴a=-
或a=0或a=2.
| 3 |
| 2 |
当B=∅时,
此时a=0,满足条件;
当B≠∅时,即a≠0,
∴B={-
| 2 |
| a |
∵A∩B=B,∴B⊆A
∴-
| 2 |
| a |
| 2 |
| a |
| 3 |
| 2 |
解得a=2或a=-
| 4 |
| 3 |
∴a=-
| 4 |
| 3 |
点评:本题重点考查集合间的子集运算,属于基础题.

练习册系列答案
相关题目
“a=2”是“关于x的不等式|x+1|+|x+2|<a的解集非空”的( )
| A、充要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既不充分又不必要条件 |
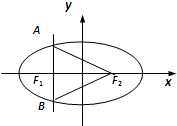 已知点F1、F2分别是椭圆
已知点F1、F2分别是椭圆 如图所示的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=2AB,CE与平面ACD所成角为45°,F、H分别为CD、DE中点.
如图所示的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=2AB,CE与平面ACD所成角为45°,F、H分别为CD、DE中点.