题目内容
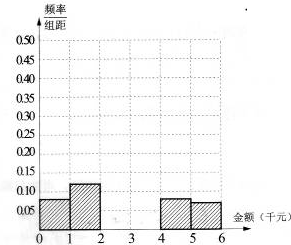 某网络营销部门随机抽查了某市200名网友在2013年11月11日的网购金额,所得数据如下表:
某网络营销部门随机抽查了某市200名网友在2013年11月11日的网购金额,所得数据如下表:| 网购金额(单位:千元) | 人数 | 频率 |
| (0,1] | 16 | 0.08 |
| (1,2] | 24 | 0.12 |
| (2,3] | x | p |
| (3,4] | y | q |
| (4,5] | 16 | 0.08 |
| (5,6] | 14 | 0.07 |
| 合计 | 200 | 1.00 |
(1)试确定x,y,p,q的值,并补全频率分布直方图(如图).
(2)该营销部门为了了解该市网友的购物体验,从这200网友中,用分层抽样的方法从网购金额在(1,2]和(4,5]的两个群体中确定5人中进行问卷调查,若需从这5人中随机选取2人继续访谈,则此2人来自不同群体的概率是多少?
考点:古典概型及其概率计算公式,频率分布直方图
专题:概率与统计
分析:(1)由网友和为200,网购金额不超过3千元与超过3千元的人数比恰为3:2列方程组求解x,y的值,则p,q可求,进一步补全频率分布直方图;
(2)分别求出从网购金额在(1,2]和(4,5]的两个群体中的人数并标记,然后用枚举法列出从5人中随机选取2人的所有不同方法数,查出2人来自不同群体的方法数,最后由古典概型概率计算公式求解.
(2)分别求出从网购金额在(1,2]和(4,5]的两个群体中的人数并标记,然后用枚举法列出从5人中随机选取2人的所有不同方法数,查出2人来自不同群体的方法数,最后由古典概型概率计算公式求解.
解答:
解:(1)根据题意有:
,解得
.
∴P=0.4,q=0.25.
补全频率分布直方图如图,
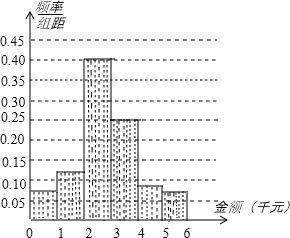
(2)根据题意,网购金额在(1,2]内的人数为
×5=3(人),记为:a,b,c.
网购金额在(4,5]内的人数为
×5=2(人),记为:A,B.
则从这5人中随机选取2人的选法为:(a,b),(a,c),(a,A),(a,B),(b,c),(b,A),
(b,B),(c,A),(c,B),(A,B)共10种.
记2人来自不同群体的事件为M,则M中含有(a,A),(a,B),(b,A),(b,B),(c,A),(c,B)共6种.
∴P(M)=
=
.
|
|
∴P=0.4,q=0.25.
补全频率分布直方图如图,

(2)根据题意,网购金额在(1,2]内的人数为
| 24 |
| 24+16 |
网购金额在(4,5]内的人数为
| 16 |
| 24+16 |
则从这5人中随机选取2人的选法为:(a,b),(a,c),(a,A),(a,B),(b,c),(b,A),
(b,B),(c,A),(c,B),(A,B)共10种.
记2人来自不同群体的事件为M,则M中含有(a,A),(a,B),(b,A),(b,B),(c,A),(c,B)共6种.
∴P(M)=
| 6 |
| 10 |
| 3 |
| 5 |
点评:本题主要考查频率分布直方图,分层抽样,古典概型等基础知识,考查学生数据处理和数据分析、运算求解能力和应用知识、或然与必然思想方法的理解程度.是中档题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
“a=2”是“关于x的不等式|x+1|+|x+2|<a的解集非空”的( )
| A、充要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既不充分又不必要条件 |
 参加市数学调研抽测的某校高三学生成绩分析的茎叶图和频率分布直方图均受到不同程度的破坏,但可见部分信息如下,据此解答如下问题:
参加市数学调研抽测的某校高三学生成绩分析的茎叶图和频率分布直方图均受到不同程度的破坏,但可见部分信息如下,据此解答如下问题: