题目内容
已知数列{an},Tn为其前n项和,且Tn+
an=1.
(1)求a1,a2,a3,并猜想{an}的通项公式;
(2)用数学归纳法证明.
| 1 |
| 2 |
(1)求a1,a2,a3,并猜想{an}的通项公式;
(2)用数学归纳法证明.
考点:数学归纳法
专题:证明题,点列、递归数列与数学归纳法
分析:(1)依题意,可求得a1=
,a2=
,a3=
;从而可猜想an=
;
(2)利用数学归纳法证明:①当n=1时,a1=
,结论成立;②假设n=k时,结论成立,即ak=
,用上归纳假设,去证明当n=k+1时结论也成立即可.
| 2 |
| 3 |
| 2 |
| 32 |
| 2 |
| 33 |
| 2 |
| 3n |
(2)利用数学归纳法证明:①当n=1时,a1=
| 2 |
| 3 |
| 2 |
| 3k |
解答:
解:(1)∵T1+
a1=1,T1=a1,
∴a1=
;
又(a1+a2)+
a2=1,
∴
a2=1-a1=
,
∴a2=
=
;
同理可求,a3=
;
∴猜想:an=
;
(2)证明:①当n=1时,a1=
,结论成立;
②假设n=k时,结论成立,即ak=
,
则当n=k+1时,(a1+a2+…+ak+ak+1)+
ak+1=1,
即Tk+
ak+1=1,
∴
ak+1=1-Tk;
∵数列{ak}是以
为首项,
为公比的等比数列,
∴Tk=
=1-(
)k,
∴
ak+1=1-1+(
)k,
∴ak+1=2•(
)k+1=
,
即n=k+1时,结论也成立;
综合①②知,对任意n∈N*,an=
.
| 1 |
| 2 |
∴a1=
| 2 |
| 3 |
又(a1+a2)+
| 1 |
| 2 |
∴
| 3 |
| 2 |
| 1 |
| 3 |
∴a2=
| 2 |
| 9 |
| 2 |
| 32 |
同理可求,a3=
| 2 |
| 33 |
∴猜想:an=
| 2 |
| 3n |
(2)证明:①当n=1时,a1=
| 2 |
| 3 |
②假设n=k时,结论成立,即ak=
| 2 |
| 3k |
则当n=k+1时,(a1+a2+…+ak+ak+1)+
| 1 |
| 2 |
即Tk+
| 3 |
| 2 |
∴
| 3 |
| 2 |
∵数列{ak}是以
| 2 |
| 3 |
| 1 |
| 3 |
∴Tk=
| ||||
1-
|
| 1 |
| 3 |
∴
| 3 |
| 2 |
| 1 |
| 3 |
∴ak+1=2•(
| 1 |
| 3 |
| 2 |
| 3k+1 |
即n=k+1时,结论也成立;
综合①②知,对任意n∈N*,an=
| 2 |
| 3n |
点评:本题考查数列递推,着重考查数学归纳法,考查运算、猜想、推理与证明的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
 如图所示的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=2AB,CE与平面ACD所成角为45°,F、H分别为CD、DE中点.
如图所示的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=2AB,CE与平面ACD所成角为45°,F、H分别为CD、DE中点.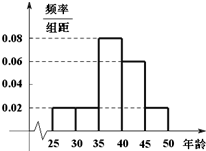 某单位N名员工参加“社区低碳你我他”活动.他们的年龄在25岁至50岁之间.按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.下表是年龄的频率分布表.
某单位N名员工参加“社区低碳你我他”活动.他们的年龄在25岁至50岁之间.按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.下表是年龄的频率分布表.