题目内容
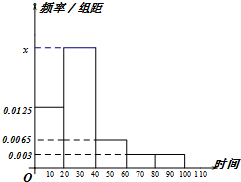 某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].(1)求直方图中x的值;
(2)如果上学路上所需时间不少于40分钟的学生可申请在学校住宿,请估计学校1000名新生中有多少名学生可以申请住宿.
考点:用样本的频率分布估计总体分布,频率分布直方图
专题:概率与统计
分析:(1)根据频率分布直方图的小矩形的面积和为1,求得x值;
(2)利用频率分布直方图先求上学所需时间不少于40的学生的频率,再利用频率乘以总体个数可得1000名新生中有多少名学生可以申请住宿.
(2)利用频率分布直方图先求上学所需时间不少于40的学生的频率,再利用频率乘以总体个数可得1000名新生中有多少名学生可以申请住宿.
解答:
解:(1)由(x+0.0125+0.0065+0.003×2)×20=1,
解得x=0.025;
(2)上学所需时间不少于40的学生的频率为:(0.0065+0.003×2)×20=0.25,
估计学校1000名新生中有:1000×0.25=250,
答:估计学校1000名新生中有250名学生可以申请住宿.
解得x=0.025;
(2)上学所需时间不少于40的学生的频率为:(0.0065+0.003×2)×20=0.25,
估计学校1000名新生中有:1000×0.25=250,
答:估计学校1000名新生中有250名学生可以申请住宿.
点评:本题考查了频率分布直方图,读懂频率分布直方图的数据含义是关键.

练习册系列答案
相关题目