题目内容
8．圆x2+（y+1）2=3绕直线kx-y-1=0旋转一周所得的几何体的表面积为12π．分析 直线恒过圆心，推知旋转体为球，求出球的半径，可求球的表面积．
解答 解：显然直线过圆心（0，-1），故旋转一周所得几何体为球，球的半径为$\sqrt{3}$，
∴S球=4πR2=4π•3=12π．
故答案为12π．
点评 本题考查旋转体的知识，直线与圆的位置关系，考查计算能力，空间想象能力，是基础题．
练习册系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
18．已知抛物线C：y2=4x的焦点为F，准线为l，P是l上一点，Q是直线PF与C的一个交点，若$\overrightarrow{FP}=5\overrightarrow{FQ}$，则|QF|=（ ）
| A． | $\frac{7}{2}$ | B． | $\frac{8}{5}$ | C． | $\frac{5}{2}$ | D． | 2 |
3．运行下面的程序中，若输入x的值为5，则输出的y的值为（ ）
| A． | 16 | B． | 17 | C． | 18 | D． | 19 |
13．执行如图的程序框图，则输出S的值为（ ）
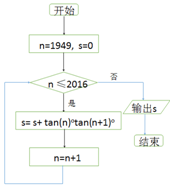
| A． | $\frac{tan2017°-tan1949°}{tan1°}$-67 | B． | $\frac{tan2016°-tan1949°}{tan1°}$-67 | ||
| C． | $\frac{tan2017°-tan1949°}{tan1°}$-68 | D． | $\frac{tan2016°-tan1949°}{tan1°}$-68 |
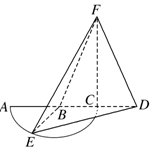如图，以AC=2为直径的⊙B，点E为$\widehat{AC}$的中点，点D在直径AC延长线上，CD=1，FC⊥平面BED，FC=2．
17．在等差数列{an}中，an＞0，且a1+a2+…+a10=30，则a5+a6的值（ ）
| A． | 3 | B． | 6 | C． | 9 | D． | 12 |
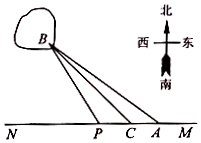如图，已知A，B两镇分别位于东西湖岸MN的A处和湖中小岛的B处，点C在A的正西方向1km处，tan∠BAN=$\frac{3}{4}$，∠BCN=$\frac{π}{4}$，现计划铺设一条电缆联通A，B两镇，有两种铺设方案：①沿线段AB在水下铺设；②在湖岸MN上选一点P，先沿线段AP在地下铺设，再沿线段PB在水下铺设，预算地下、水下的电缆铺设费用分别为2万元∕km、4万元∕km．