题目内容
20.已知椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{9}$=1,若P(x,y)是椭圆C上一动点,则x2+y2-2x的取值范围是( )| A. | [6-2$\sqrt{6}$,9] | B. | [6-2$\sqrt{6}$,11] | C. | [6+2$\sqrt{6}$,9] | D. | [6+2$\sqrt{6}$,11] |
分析 P(x,y)满足椭圆方程,整理得到x2+y2-2x=-$\frac{1}{2}$(x+2)2+11,进而得到x2+y2-2x的取值范围
解答 解:∵P(x,y)是椭圆C上一动点,
∴$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{9}$=1,
∴x2+y2-2x=x2+9-$\frac{3}{2}$x2-2x=-$\frac{1}{2}$x2-2x+9=-$\frac{1}{2}$(x+2)2+11,
∵-$\sqrt{6}$≤x≤$\sqrt{6}$,
∴当x=-2时,有最大值,最大值为11,
当x=$\sqrt{6}$时,有最小值,最小值为6-2$\sqrt{6}$,
故选:B
点评 本题考查椭圆的标准方程,考查了二次函数的性质,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.在等差数列{an}中,an>0,且a1+a2+…+a10=30,则a5+a6的值( )
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
8.已知双曲线$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线平行于直线l:y=x+10,双曲线的一个焦点在直线l上,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{20}$=1 | B. | $\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{5}$=1 | C. | y2-x2=50 | D. | x2-y2=10 |
5.不等式(x+1)(x-2)>0的解集为( )
| A. | {x|x<-1或x>2} | B. | {x|x<-2或x>1} | C. | {x|-2<x<1} | D. | {x|-1<x<2} |
10.设△ABC的内角A、B、C的对边分别为a、b、c,且A=60°,b=1,△ABC的面积S△ABC=$\frac{{\sqrt{3}}}{2}$,则$\frac{a+b+c}{sinA+sinB+sinC}$=( )
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | 2 | D. | 4 |
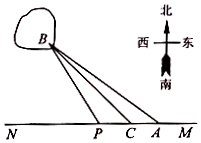 如图,已知A,B两镇分别位于东西湖岸MN的A处和湖中小岛的B处,点C在A的正西方向1km处,tan∠BAN=$\frac{3}{4}$,∠BCN=$\frac{π}{4}$,现计划铺设一条电缆联通A,B两镇,有两种铺设方案:①沿线段AB在水下铺设;②在湖岸MN上选一点P,先沿线段AP在地下铺设,再沿线段PB在水下铺设,预算地下、水下的电缆铺设费用分别为2万元∕km、4万元∕km.
如图,已知A,B两镇分别位于东西湖岸MN的A处和湖中小岛的B处,点C在A的正西方向1km处,tan∠BAN=$\frac{3}{4}$,∠BCN=$\frac{π}{4}$,现计划铺设一条电缆联通A,B两镇,有两种铺设方案:①沿线段AB在水下铺设;②在湖岸MN上选一点P,先沿线段AP在地下铺设,再沿线段PB在水下铺设,预算地下、水下的电缆铺设费用分别为2万元∕km、4万元∕km.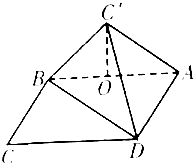 如图.在矩形ABCD中.AB=3 $\sqrt{3}$,BC=3,沿对角线BD把△BCD折起.使C移到C′.且C′在面ABC内的射影O恰好落在AB上.
如图.在矩形ABCD中.AB=3 $\sqrt{3}$,BC=3,沿对角线BD把△BCD折起.使C移到C′.且C′在面ABC内的射影O恰好落在AB上.