Question

1．《数学万花筒》第7页中谈到了著名的“四色定理”．问题起源于1852年的伦敦大学学院毕业生弗朗西斯•加斯里．他给自己的弟弟弗莱德里克写了一封信，信中提到了他认为应该很简单的一道小谜题．他一直尝试着给一张英国各郡的地图着色，在这个过程中，他发现使用四中颜色就可以实现他的目的，即使相邻的两个郡具有不同的颜色．“可以使用四种（或更少）颜色为平面上画出的每张地图着色，使任何相邻的两个地区的边界线具有不同的颜色吗？”他写道．
回答他这个问题用了124年．而且，即使现在，答案也依赖于大量的计算机辅助．目前还不知道四色原理的简单的概念性证明．但较简单的图形还是能够一步步检查得出．如：
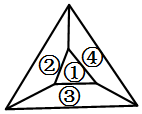
若用红、黄、蓝、绿四种颜色给右边的地图着色，共有24种着色方法．

Answer 1

分析 使用分步乘法计数原理计算．

解答 解：第一步，给区域①涂色，共有4种选择方法；
第二步，给区域②涂色，共有3种选择方法；
第三步，给区域③涂色，共有2种选择方法；
第四部，给区域④涂色，只有1种选择方法；
∴共有4×3×2×1=24种方法．
故答案为24．

点评 本题考查了分步乘法计数原理，属于基础题．