题目内容
已知在三棱锥OABC中,
•
=
•
=
•
,点G是定点O在底面ABC内的投影,则G为△ABC的 .
| OA |
| OB |
| OA |
| OC |
| OB |
| OC |
考点:向量在几何中的应用
专题:综合题,平面向量及应用
分析:判断OA⊥CB,OB⊥CA,OC⊥AB,利用点G是定点O在底面ABC内的投影,可得G为△ABC的垂心.
解答:
解:∵
•
=
•
,
∴
•
=0,
∴OA⊥CB,
同理OB⊥CA,OC⊥AB,
∵点G是定点O在底面ABC内的投影,
∴G为△ABC的垂心.
故答案为:垂心.
| OA |
| OB |
| OA |
| OC |
∴
| OA |
| CB |
∴OA⊥CB,
同理OB⊥CA,OC⊥AB,
∵点G是定点O在底面ABC内的投影,
∴G为△ABC的垂心.
故答案为:垂心.
点评:本题考查向量在几何中的应用,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
已知集合A={3,5,6,8},B={1,3,5},那么A∪B等于( )
| A、{1,3,5,6,8} |
| B、{6,8} |
| C、{3,5} |
| D、{1,6,8} |
已知
,
为平面向量,若
+
与
的夹角为60°,
+
与
的夹角为45°,则|
|与|
|之比为( )
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| b |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,正四棱锥S-ABCD,底面边长与高都是2,K是SC的中点,T是SB的中点.
如图,正四棱锥S-ABCD,底面边长与高都是2,K是SC的中点,T是SB的中点.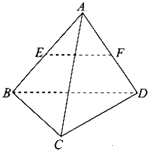 如图,四面体ABCD的每条棱长都等于2,点E,F分别为棱AB,AD的中点,则|
如图,四面体ABCD的每条棱长都等于2,点E,F分别为棱AB,AD的中点,则|