题目内容
已知
=(3,1),
=(2,4),|
|=1,点C在OA上的射影为点D,则|
|的最大值为 .
| OA |
| OB |
| BC |
| OD |
考点:平面向量的坐标运算,向量的模
专题:平面向量及应用
分析:据已知得到C在一圆上,将OD的最大值转化为OB在直线OA上的投影+半径长度;利用向量垂直的充要条件判断出OA与AB垂直求出最大值.
解答:
解:BC的长度为1,点C在以点B(2,4)为圆心,以r=1为半径的圆上,
连接BA,
=(3,1),
=(2,4),
∴
=(-1,3)
∵
•
=3×(-1)+1×3=0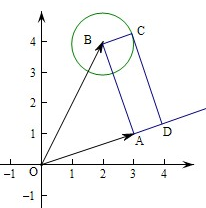
∴
⊥
,
即AB⊥OA,
由圆的性质可知,当点C位于图中位置时,过点C作OA的垂线交OA于D,此时|
|取得最大值,
即|
|最大值=|
|+1=
+1
故答案为:
+1
连接BA,
| OA |
| OB |
∴
| AB |
∵
| OA |
| AB |

∴
| OA |
| AB |
即AB⊥OA,
由圆的性质可知,当点C位于图中位置时,过点C作OA的垂线交OA于D,此时|
| OD |
即|
| OD |
| OA |
| 10 |
故答案为:
| 10 |
点评:本题考查等价转化的能力、向量的运算法则及向量垂直的充要条件.

练习册系列答案
相关题目
函数f(x)=
,满足对任意定义域中的x1,x2(x1≠x2),[f(x1)-f(x2)](x1-x2)<0总成立,则实数a的取值范围是( )
|
| A、(-∞,0) |
| B、[-1,0) |
| C、(-1,0) |
| D、(-1,+∞), |
