题目内容

正四面体ABCD的棱长为4，E为棱BC的中点，过E作其外接球的截面，则截面面积的最小值为
 
．
考点：球内接多面体
专题：计算题,空间位置关系与距离,球
分析：根据题意，将四面体ABCD放置于如图所示的正方体中，则正方体的外接球就是四面体ABCD的外接球．因此利用题中数据算出外接球半径R=
6
，过E点的截面到球心的最大距离为
2
，再利用球的截面圆性质可算出截面面积的最小值．
解答： 解：将四面体ABCD放置于正方体中，如图所示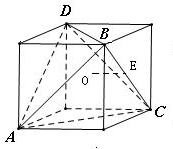
可得正方体的外接球就是四面体ABCD的外接球，
∵正四面体ABCD的棱长为4，
∴正方体的棱长为2
2
，
可得外接球半径R满足2R=2
2
•
3
，解得R=
6

E为棱BC的中点，过E作其外接球的截面，当截面到球心O的距离最大时，
截面圆的面积达最小值，
此时球心O到截面的距离等于正方体棱长的一半，
可得截面圆的半径为r=
R2-2
=2，得到截面圆的面积最小值为S=πr2=4π．
故答案为：4π
点评：本题给出正四面体的外接球，求截面圆的面积最小值．着重考查了正方体的性质、球内接多面体和球的截面圆性质等知识，属于中档题．
练习册系列答案
相关题目
点P（1，-2）到抛物线y2=4x的焦点F的距离为
 
．
以下推断中，m，n是直线，α，β是平面，则所有正确的命题有
 
（写出序号）．
①
α⊥β
m⊥β
⇒m∥α
②
m⊥β
m∥n
⇒n⊥β
③
α∥β
m⊥β
⇒m⊥α
④
α⊥β
m?β
⇒m⊥α．
已知
OA
=（3，1），
OB
=（2，4），|
BC
|=1，点C在OA上的射影为点D，则|
OD
|的最大值为
 
．
已知函数f（x）=ax2+ax+1，若f（x）＞0恒成立，则实数a的取值范围为
 
．
中心在坐标原点，焦点在y轴上的双曲线的渐近线过点P（2，1），其离心率为
 
．
已知函数f（x）=xln x．若对所有x≥1都有f（x）≥ax-1，则实数a的取值范围为
 
．
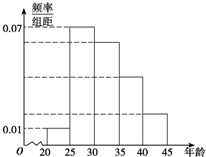如图是依据某城市年龄在20岁到45岁的居民上网情况调查而绘制的频率分布直方图，现已知年龄在[30，35）、[35，40）、[40，45]的上网人数呈现递减的等差数列分布，则年龄在[35，40）的网民出现的频率为（　　）
A、0.04B、0.06
C、0.2D、0.3
设随机变量ξ的分布列如下：
ξ -1 0 1
P a b c
其中a，b，c成等差数列，若E（ξ）=
1
3
，则D（3ξ-1）=（　　）
A、4
B、
5
3
C、
2
3
D、5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网