题目内容

椭圆
x2
4
+
3y2
4
=1上点P（1，1）处的切线方程是
 
．
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：由椭圆
x2
4
+
3y2
4
=1，可得y＞0时，y=
4
3
-
x2
3
，求导函数，求出切线的斜率，即可得出切线方程．
解答： 解：∵椭圆
x2
4
+
3y2
4
=1，
∴y＞0时，y=
4
3
-
x2
3
，
∴y′=
-
2
3
x
2
4
3
-
x2
3
，
∴x=1时，y′=-
1
3
，
∴椭圆
x2
4
+
3y2
4
=1上点P（1，1）处的切线方程是y-1=-
1
3
（x-1），即x+3y-4=0．
故答案为：x+3y-4=0．
点评：本题考查导数知识的运用，考查导数的几何意义，正确求出切线的斜率是关键．
练习册系列答案
相关题目
已知函数f（x）=ex-ax-1（a＞0，e为自然对数的底数）．
（1）求函数f（x）的最小值；
（2）若f（x）≥0对任意的x∈R恒成立，求实数a的值．
点P（1，-2）到抛物线y2=4x的焦点F的距离为
 
．
给出下列命题：
①函数y=2-|x|为偶函数；
②函数y=1是周期函数；
③函数f（x）=2x-x2的零点有2个；
④函数g（x）=|log2 x|-（
1
2
）x在（0，+∞）上恰有两个零点x1，x2且x1•x2＜1．
其中真命题的序号为
 
．
已知点P是曲线C：
x=4cosθ
y=3sinθ
（θ为参数，π≤θ≤2π）上一点，O为原点．若直线OP的倾斜角为
π
4
，则点P的直角坐标为
 
．
袋中装有黑球和白球共7个，从中任取2个球都是白球的概率为
1
7
．现有甲、乙两人从袋中轮流、不放回地摸取1球，甲先取，乙后取，然后甲再取…直到袋中的球取完即终止．若摸出白球，则记2分，若摸出黑球，则记1分．每个球在每一次被取出的机会是等可能的．用ξ表示甲四次取球获得的分数之和．
（Ⅰ）求袋中原有白球的个数；
（Ⅱ）求随机变量ξ的概率分布列及期望Eξ．
以下推断中，m，n是直线，α，β是平面，则所有正确的命题有
 
（写出序号）．
①
α⊥β
m⊥β
⇒m∥α
②
m⊥β
m∥n
⇒n⊥β
③
α∥β
m⊥β
⇒m⊥α
④
α⊥β
m?β
⇒m⊥α．
已知
OA
=（3，1），
OB
=（2，4），|
BC
|=1，点C在OA上的射影为点D，则|
OD
|的最大值为
 
．
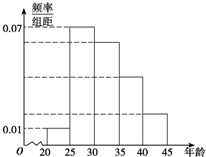如图是依据某城市年龄在20岁到45岁的居民上网情况调查而绘制的频率分布直方图，现已知年龄在[30，35）、[35，40）、[40，45]的上网人数呈现递减的等差数列分布，则年龄在[35，40）的网民出现的频率为（　　）
A、0.04B、0.06
C、0.2D、0.3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网