题目内容
若曲线y=
与直线y=k(x-2)+3有两个不同的公共点,则实数k的取值范围是 .
| 4-x2 |
考点:直线与圆的位置关系,圆的切线方程
专题:直线与圆
分析:直线y=k(x-2)+3过点P(2,3),求出两个特殊位置直线的斜率,可得结论.
解答:
 解:由题意,直线y=k(x-2)+3过定点P(2,3),
解:由题意,直线y=k(x-2)+3过定点P(2,3),
曲线y=
表示圆心为(0,0),半径r=2的圆的上半部分.
当直线过点(-2,0)时,直线与曲线有两个交点,
此时,斜率k=
=
.
当直线与圆相切时,圆心到直线的距离d=
=2.
解得,k=
.
∴实数k的取值范围是(
,
].
故答案为:(
,
].
 解:由题意,直线y=k(x-2)+3过定点P(2,3),
解:由题意,直线y=k(x-2)+3过定点P(2,3),曲线y=
| 4-x2 |
当直线过点(-2,0)时,直线与曲线有两个交点,
此时,斜率k=
| 3-0 |
| 2-(-2) |
| 3 |
| 4 |
当直线与圆相切时,圆心到直线的距离d=
| |3-2k| | ||
|
解得,k=
| 5 |
| 12 |
∴实数k的取值范围是(
| 5 |
| 12 |
| 3 |
| 4 |
故答案为:(
| 5 |
| 12 |
| 3 |
| 4 |
点评:本题考查直线与圆的位置关系,圆的切线方程的应用,考查数形结合以及计算能力.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
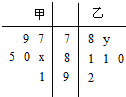 某学校从高二甲、乙两个班中各选6名同掌参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的众数是85,乙班学生成绩的平均分为81,则x+y的值为( )
某学校从高二甲、乙两个班中各选6名同掌参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的众数是85,乙班学生成绩的平均分为81,则x+y的值为( )| A、6 | B、7 | C、8 | D、9 |
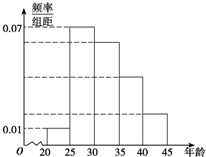 如图是依据某城市年龄在20岁到45岁的居民上网情况调查而绘制的频率分布直方图,现已知年龄在[30,35)、[35,40)、[40,45]的上网人数呈现递减的等差数列分布,则年龄在[35,40)的网民出现的频率为( )
如图是依据某城市年龄在20岁到45岁的居民上网情况调查而绘制的频率分布直方图,现已知年龄在[30,35)、[35,40)、[40,45]的上网人数呈现递减的等差数列分布,则年龄在[35,40)的网民出现的频率为( )| A、0.04 | B、0.06 |
| C、0.2 | D、0.3 |
若数列{an}的前n项和为Sn,有下列命题:
(1)若数列{an}的极限存在但不为零,则数列{Sn}的极限一定不存在;
(2)无穷数列{S2n}、{S2n-1}的极限均存在,则数列{Sn}的极限一定存在;
(3)若{an}是等差数列(公差d≠0),则S1•S2•…•Sk=O的充要条件是a1•a2•…•ak=O;
(4)若{an}是等比数列,则S1•S2•…•Sk=O(k≥2)的充要条件是an+an+1=0.
其中,错误命题的序号是( )
(1)若数列{an}的极限存在但不为零,则数列{Sn}的极限一定不存在;
(2)无穷数列{S2n}、{S2n-1}的极限均存在,则数列{Sn}的极限一定存在;
(3)若{an}是等差数列(公差d≠0),则S1•S2•…•Sk=O的充要条件是a1•a2•…•ak=O;
(4)若{an}是等比数列,则S1•S2•…•Sk=O(k≥2)的充要条件是an+an+1=0.
其中,错误命题的序号是( )
| A、(1)(2) |
| B、(2)(3) |
| C、(3)(4) |
| D、(1)(4) |
等比数列{an}的各项为正数,且3是a5和a6的等比中项,则a1a2…a10=( )
| A、39 |
| B、310 |
| C、311 |
| D、312 |