题目内容
在△ABC中角A,B,C所对的边分别为a,b,c已知cos
=
,
(1)求cosC的值;
(2)若acosB+bcosA=2,a=
,求sinA的值.
| C |
| 2 |
| ||
| 3 |
(1)求cosC的值;
(2)若acosB+bcosA=2,a=
| 2 |
考点:余弦定理,正弦定理
专题:三角函数的求值,解三角形
分析:(1)由二倍角的余弦公式代入已知即可求cosC的值.
(2)由已知及余弦定理可得a×
+b×
=2,从而解得c的值,求得sinC的值,即可由正弦定理求得sinA的值.
(2)由已知及余弦定理可得a×
| a2+c2-b2 |
| 2ac |
| c2+b2-a2 |
| 2bc |
解答:
解:(1)∵cos
=
,
∴cosC=2cos2
-1=2(
)2-1=
.
(2)∵acosB+bcosA=2,
∴由余弦定理可得:a×
+b×
=2,
∴从而解得:c=2,
又∵a=
,cosC=
,
∴sinC=
=
,
∴由
=
得sinA=
=
=
.
| C |
| 2 |
| ||
| 3 |
∴cosC=2cos2
| C |
| 2 |
| ||
| 3 |
| 1 |
| 9 |
(2)∵acosB+bcosA=2,
∴由余弦定理可得:a×
| a2+c2-b2 |
| 2ac |
| c2+b2-a2 |
| 2bc |
∴从而解得:c=2,
又∵a=
| 2 |
| 1 |
| 9 |
∴sinC=
| 1-cos2C |
4
| ||
| 9 |
∴由
| c |
| sinC |
| a |
| sinA |
| asinC |
| c |
| ||||||
| 2 |
2
| ||
| 9 |
点评:本题主要考察了正弦定理、余弦定理的综合应用,考察了二倍角的余弦公式的应用,属于基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
半径为R的球内接一个正方体,则该正方体的体积是( )
A、
| ||||
B、
| ||||
C、2
| ||||
| D、8R3 |
已知幂函数y=f(x)的图象过点(3,
),则f(9)=( )
| 3 |
| A、3 | ||
| B、-3 | ||
C、-
| ||
D、
|
在△ABC中,已知△ABC的面积为S=a2-(b-c)2,则有( )
| A、sinA-4cosA=4 |
| B、sinA+4cosA=4 |
| C、cosA-4sinA=4 |
| D、cosA+4sinA=4 |
在如下程序框图中,输入f0(x)=xex,若输出的fi(x)是(8+x)ex,则程序框图中的判断框应填入( )
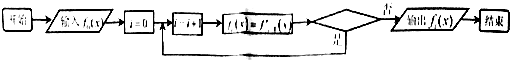
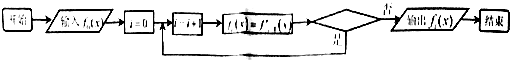
| A、i≤6 | B、i≤7 |
| C、i≤8 | D、i≤9 |
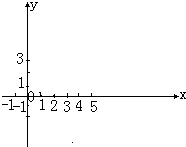 已知函数f(x)=
已知函数f(x)=