题目内容
将1，2，3，…，9这9个正整数分别写在三张卡片上，要求每一张卡片上的任意两数之差都不在这张卡片上．现在第一张卡片上已经写有1和5，第二张卡片上写有2，第三张卡片上写有3，则6应该写在第 张卡片上；第三张卡片上的所有数组成的集合是 ．
考点：计数原理的应用
专题：排列组合
分析：根据每一张卡片上的任意两数之差都不在这张卡片上，第一张卡片上已经写有1和5，第二张卡片上写有2，第三张卡片上写有3，即可得出结论．
解答：
解：由题意，∵要求每一张卡片上的任意两数之差都不在这张卡片上，第一张卡片上已经写有1和5，第二张卡片上写有2，第三张卡片上写有3，
∴4、9写在第三张卡片上，6、8在第二张卡片上，
故答案为：二；{3，4，9}．
∴4、9写在第三张卡片上，6、8在第二张卡片上，
故答案为：二；{3，4，9}．
点评：本题考查计数原理的运用，考查学生分析解决问题的能力，属于基础题．
练习册系列答案
全能测控期末小状元系列答案
相关题目
已知圆O：x2+y2=4（O为坐标原点），点P（1，0），现向圆O内随机投一点A，则点P到直线OA的距离小于
的概率为（ ）
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f（x）=Asin（ωx+φ）（A，ω，φ为常数，A＞0，ω＞0，0＜φ＜π）的图象如图所示，则f（
如图，转盘被分成了4部分，其中∠AOB=∠COD=90°，则随意转动转盘，指针指向∠AOB和∠COD所在区域的概率是已知A（2，1），B（1，-2），C（
，-
），动点P（a，b）满足0≤
•
≤2且0≤
•
≤2，则点P到点C的距离大于
的概率为（ ）
| 3 |
| 5 |
| 1 |
| 5 |
| OP |
| OA |
| OP |
| OB |
| 1 |
| 4 |
A、1-
| ||
B、
| ||
C、1-
| ||
D、
|
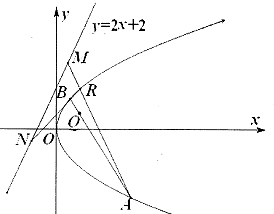已知抛物线C的方程为y2=2px（p＞0），点R（1，2）在抛物线C上．