题目内容
已知函数f(x)=|x-a|(a>0),且不等式f(x)≥|x+1|的解集为{x|x≤
}.
(Ⅰ)求a的值;
(Ⅱ)设函数g(x)=f(x)+|2x+1|,若不等式|2m+n|+|m-n|≥|m|•g(x)对任意m,n∈R且m≠0恒成立,求x的取值范围.
| 1 |
| 2 |
(Ⅰ)求a的值;
(Ⅱ)设函数g(x)=f(x)+|2x+1|,若不等式|2m+n|+|m-n|≥|m|•g(x)对任意m,n∈R且m≠0恒成立,求x的取值范围.
考点:绝对值不等式的解法
专题:函数的性质及应用,不等式的解法及应用
分析:(Ⅰ)化简不等式为绝对值不等式利用数轴推出结果即可.
(Ⅱ)转化不等式,利用绝对值三角不等式,求出表达式的最小值,通过恒成立求出x的范围即可.
(Ⅱ)转化不等式,利用绝对值三角不等式,求出表达式的最小值,通过恒成立求出x的范围即可.
解答:
解:(Ⅰ)由不等式f(x)≥|x+1|可得|x-a|≥|x+1|,
∵a>0,由数轴可知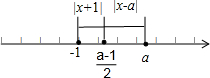 ∴解得x≤
∴解得x≤
,
∵不等式f(x)≥|x+1|的解集为{x|x≤
}.
∴
=
,得a=2.
(Ⅱ)由(Ⅰ)得g(x)=|x-2|+|2x+1|,
又不等式|2m+n|+|m-n|≥|m|•g(x)
∴
≥g(x),
而
≥
=3,
∴g(x)≤3恒成立,
即|x-2|+|2x+1|≤3,
解得x的取值范围:{x|-
≤x≤0}.
∵a>0,由数轴可知
 ∴解得x≤
∴解得x≤| a-1 |
| 2 |
∵不等式f(x)≥|x+1|的解集为{x|x≤
| 1 |
| 2 |
∴
| 1 |
| 2 |
| a-1 |
| 2 |
(Ⅱ)由(Ⅰ)得g(x)=|x-2|+|2x+1|,
又不等式|2m+n|+|m-n|≥|m|•g(x)
∴
| |2m+n|+|m-n| |
| |m| |
而
| |2m+n|+|m-n| |
| |m| |
| |2m+n+m-n| |
| |m| |
∴g(x)≤3恒成立,
即|x-2|+|2x+1|≤3,
解得x的取值范围:{x|-
| 2 |
| 3 |
点评:本题考查绝对值不等式的解法,函数恒成立问题的应用,考查转化思想以及计算能力.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
给出程序框图,若输入的x值为-5,则输出的y的值是( )


| A、-2 | B、-1 | C、0 | D、1 |
在区间[0,2]之间随机抽取一个数x,则x满足2x-1≥0的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,已知椭圆
如图,已知椭圆 如图所示,边长为2的正方形中有一封闭曲线围成的阴影区域,在正方形中随机撒一粒豆子,若它落在阴影区域内的概率为
如图所示,边长为2的正方形中有一封闭曲线围成的阴影区域,在正方形中随机撒一粒豆子,若它落在阴影区域内的概率为