题目内容
19．已知圆C：（x-1）2+（y-4）2=10和点M（5，t），若圆C上存在两点A，B，使得MA⊥MB，则实数t的取值范围为（ ）| A． | [-2，6] | B． | [-3，5] | C． | [2，6] | D． | [3，5] |
分析 由题意，|CM|≤$\sqrt{10}×\sqrt{2}$，即可求出实数t的取值范围．
解答 解：由题意，|CM|≤$\sqrt{10}×\sqrt{2}$，
∴（5-1）2+（t-4）2≤20，
∴2≤t≤6，
故选C．
点评 本题考查直线与圆的位置关系，考查学生的计算能力，正确转化是关键．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
8．已知函数f（x）=x2+m与函数g（x）=-ln$\frac{1}{x}-3x（{x∈[{\frac{1}{2}，2}]}）$的图象上恰有两对关于x轴对称的点，则实数m的取值范围是（ ）
| A． | $[{\frac{5}{4}+ln2，2}）$ | B． | $[{2-ln2，\frac{5}{4}+ln2}）$ | C． | $（{\frac{5}{4}+ln2，2-ln2}]$ | D． | （2-ln2，2] |
7．一个盒中装有编号分别为1，2，3，4的四个形状大小完全相同的小球，从盒中任取一球，记下该球的编号后，将球放回，再从盒中任取一球，记下该球的编号，把两次取球的编号a，b分别作为点P的横、纵坐标，则点P（a，b）落在直线x+y=4下方的概率为（ ）
| A． | $\frac{1}{8}$ | B． | $\frac{3}{16}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |
14．已知集合M={1，2}，N={2，3，4}，若P=M∪N，则P的子集个数为（ ）
| A． | 14 | B． | 15 | C． | 16 | D． | 32 |
4．过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别作它的两条渐近线的平行线，若这4条直线所围成的四边形的周长为8b，则该双曲线的渐近线方程为（ ）
| A． | y=±x | B． | y=±$\sqrt{2}$x | C． | y=±$\sqrt{3}$x | D． | y=±2x |
11．已知向量$\overrightarrow{a}$=（x-z，1），$\overrightarrow{b}$=（2，y+z），且$\overrightarrow{a}$⊥$\overrightarrow{b}$，若实数x，y满足不等式组$\left\{\begin{array}{l}{y-x≥0}\\{x+y-7≤0}\\{x≥0}\end{array}\right.$，则z的最大值为（ ）
| A． | $\frac{21}{2}$ | B． | 7 | C． | 14 | D． | 21 |
8．下列说法正确的是（ ）
| A． | 命题“?x0∈R+，x02-x0＜0”的否定是“?x∈R-，x2-x≥0” | |
| B． | 命题“若a≠b，则a2≠b2”的否命题是“若a≠b，则a2=b2” | |
| C． | x1＞1且x2＞1的充要条件是x1+x2＞2． | |
| D． | p，q为两个命题，若p∨q为真且p∧q为假，则p，q两个命题中必有一个为真，一个为假． |
9．
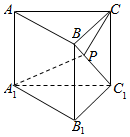如图，在三棱柱ABC-A1B1C1中，CC1⊥底面A1B1C1，且A1C1⊥B1C1，A1C1=3$\sqrt{2}$，B1C1=CC1=2，P是BC1上一动点，则CP+PA1的最小值为（ ）
如图，在三棱柱ABC-A1B1C1中，CC1⊥底面A1B1C1，且A1C1⊥B1C1，A1C1=3$\sqrt{2}$，B1C1=CC1=2，P是BC1上一动点，则CP+PA1的最小值为（ ）| A． | 5$\sqrt{2}$ | B． | 5 | C． | $\sqrt{10}$ | D． | $\sqrt{34}$ |