题目内容
4.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别作它的两条渐近线的平行线,若这4条直线所围成的四边形的周长为8b,则该双曲线的渐近线方程为( )| A. | y=±x | B. | y=±$\sqrt{2}$x | C. | y=±$\sqrt{3}$x | D. | y=±2x |
分析 过右焦点,与一条渐近线平行的直线方程为bx-ay-bc=0,令x=0,y=$\frac{bc}{a}$,利用这4条直线所围成的四边形的周长为8b,建立方程,即可得出结论.
解答 解:过右焦点,与一条渐近线平行的直线方程为bx-ay-bc=0,
令x=0,y=$\frac{bc}{a}$,
∵这4条直线所围成的四边形的周长为8b,
∴$2b=\sqrt{\frac{{b}^{2}{c}^{2}}{{a}^{2}}+{c}^{2}}$,∴a=b,
∴该双曲线的渐近线方程为y=±x,
故选A.
点评 本题考查双曲线的方程与性质,考查学生的计算能力,属于中档题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
19.已知圆C:(x-1)2+(y-4)2=10和点M(5,t),若圆C上存在两点A,B,使得MA⊥MB,则实数t的取值范围为( )
| A. | [-2,6] | B. | [-3,5] | C. | [2,6] | D. | [3,5] |
13.若θ是第二象限角且sinθ=$\frac{12}{13}$,则$tan(θ+\frac{π}{4})$=( )
| A. | $-\frac{17}{7}$ | B. | $-\frac{7}{17}$ | C. | $\frac{17}{7}$ | D. | $\frac{7}{17}$ |
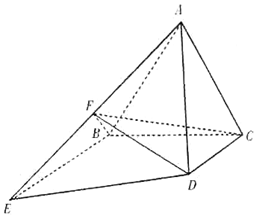 如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AE的中点.
如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AE的中点.