题目内容

已知函数y=x+5+
-x2-2x+4
，求其值域．
考点：函数的值域
专题：函数的性质及应用
分析：由y=x+5+
-x2-2x+4
得：y-x-5=
-x2-2x+4
，平方后整理得2x2+（12-2y）x+y2-10y+21=0，根据判别式法，可得△=（12-2y）2-8（y2-10y+21）≥0，解得y的范围即为函数的值域．
解答： 解：由y=x+5+
-x2-2x+4
得：y-x-5=
-x2-2x+4
，
故x2+y2+25-2xy+10x-10y=-x2-2x+4，
即2x2+（12-2y）x+y2-10y+21=0，
由△=（12-2y）2-8（y2-10y+21）≥0得：y2-8y+6≤0
解得：y∈[4-
10
，4+
10
]，
故函数y=x+5+
-x2-2x+4
的值域为[4-
10
，4+
10
]．
点评：本题考查的知识点是函数的值域，熟练掌握判断式法求函数值域的方法和步骤是解答的关键．
练习册系列答案
相关题目
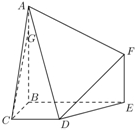如图，多面体ABCDEF中，BA、BC、BE两两垂直，且AB∥EF，CD∥BE，AB=BE=2，BC=CD=EF=1．
（Ⅰ）若点G在线段AB上，且BG=3GA，求证：CG∥平面ADF；
（Ⅱ）求证：平面ABD⊥平面DEF．
（Ⅲ）求直线DF与平面ABEF所成的角的正弦值．
已知数列{an}的前n项和为Sn，且Sn=n2+2n．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）数列{bn}中，b1=1，bn=2bn-1+1（n≥2），求{bn}的通项公式；
（Ⅲ）若cn=an（bn+1），求数列{cn}前几项和Tn．
已知双曲线C：
x2
a2
-
y2
b2
=1离心率是
2
，过点（
3
，1），且右支上的弦AB过右焦点F．
（1）求双曲线C的方程；
（2）求弦AB的中点M的轨迹E的方程；
（3）是否存在以AB为直径的圆过原点O？，若存在，求出直线AB的斜率k的值．若不存在，则说明理由．
某企业主要生产甲、乙两种品牌的空调，由于受到空调在保修期内维修费等因素的影响，企业生产每台空调的利润与该空调首次出现故障的时间有关，甲、乙两种品牌空调的保修期均为3年，现从该厂已售出的两种品牌空调中各随机抽取50台，统计数据如下：
品牌甲乙
首次出现故障时间
x年		0＜x≤11＜x≤22＜x≤3x＞30＜x≤22＜x≤3x＞3
空调数量（台）124432345
每台利润（千元）122.52.71.52.62.8
将频率视为概率，解答下列问题：
（Ⅰ）从该厂生产的甲品牌空调中随机抽取一台，求首次出现故障发生在保修期内的概率；
（Ⅱ）若该厂生产的空调均能售出，记生产一台甲品牌空调的利润为X1，生产一台乙品牌空调的利润为X2，分别求X1，X2的分布列；
（Ⅲ）该厂预计今后这两种品牌空调销量相当，但由于资金限制，只能生产其中一种品牌空调，若从经济效益的角度考虑，你认为应该生产哪种品牌的空调？说明理由．
解关于x的不等式：
x+1
x+2
≥0．
已知函数f（x），g（x）都定义在实数集R上，且满足f（x）为奇函数，g（x）为偶函数，f（x）+g（x）=x2+x-2，试求函数f（x），g（x）的解析式．
如图，在四棱锥P-ABCD中，底面ABCD是菱形，PA⊥平面ABCD，PA=AB，∠ABC=60°，E、F分别是PB，CD的中点．
（Ⅰ）证明：PB⊥面AEF
（Ⅱ）求二面角A-PE-F的大小．
四棱锥P-ABCD的底面是边长为2的菱形，且∠BAD=60°，PA⊥平面ABCD，设E为BC的中点，二面角P-DE-A为45°．
（1）求点A到平面PDE的距离；
（2）在PA上确定一点F，使BF∥平面PDE；
（3）求异面直线PC与DE所成的角（用反三角函数表示）；
（4）求面PDE与面PAB所成的不大于直二面角的二面角的大小（用反三角函数表示）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网