题目内容
在△ABC中,A,B,C所对边分别为a,b,c,则下列各式中一定成立的是( )
A、
| ||||
B、
| ||||
| C、asinB=bcosA | ||||
| D、a=2RcosA |
考点:正弦定理
专题:解三角形
分析:△ABC中,由正弦定理可得
=
,变形可得结论.
| a |
| sinA |
| b |
| sinB |
解答:
解:在△ABC中,由正弦定理可得
=
,即
=
,
故选:B.
| a |
| sinA |
| b |
| sinB |
| a |
| b |
| sinA |
| sinB |
故选:B.
点评:本题主要考查正弦定理的应用,属于基础题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
若等比数列{an}满足2a4=a6-a5,则q=( )
| A、-1或2 | B、1或-2 |
| C、0 | D、-1或-2 |
设t是实数,i是虚数单位,且
+
是实数,则t=( )
| t |
| 1+i |
| 1-i |
| 2 |
| A、-1 | B、1 | C、0 | D、2 |
已知非零向量
,
,
满足
+
+
=0,向量
与
的夹角为60°,且|
|=|
|=1,则向量
与
的夹角为( )
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| a |
| c |
| A、30° | B、60° |
| C、120° | D、150° |
已知某个几何体的三视图如图所示,根据图中数据,求这个几何体的体积是( )

A、
| ||
B、
| ||
C、
| ||
| D、2 |
将4名学生分到三个不同的班级,在每个班级至少分到一名学生的条件下,其中甲、乙两名学生不能分到同一个班级的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
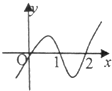
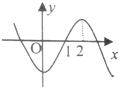
 函数y=f(x)的导函数f′(x)的图象如图所示,则y=f(x)的图象最有可能的是( )
函数y=f(x)的导函数f′(x)的图象如图所示,则y=f(x)的图象最有可能的是( )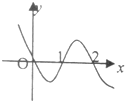

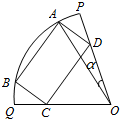 已知OPQ是半径为1,圆心角为2θ(θ为定值)的扇形,A是扇形弧上的动点,四边形ABCD是扇形内的内接矩形,记∠AOP=α(0<α<θ).
已知OPQ是半径为1,圆心角为2θ(θ为定值)的扇形,A是扇形弧上的动点,四边形ABCD是扇形内的内接矩形,记∠AOP=α(0<α<θ).