题目内容
三角形ABC中,∠C=90°,AB=2,AC=1,若
=
,则
•
=( )
| AD |
| 3 |
| 2 |
| AB |
| CD |
| CB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:平面向量数量积的运算
专题:平面向量及应用
分析:通过建立直角坐标系,利用向量的坐标运算和数量积运算即可得出.
解答:
解:如图所示,
在三角形ABC中,∠C=90°,AB=2,AC=1,
∴CB=
=
.
∴C(0,0),A(1,0),B(0,
).
∵
=
,∴
=
(-1,
)=(-
,
).
∴
=
+
=(1,0)+(-
,
)=(-
,
).
∴
•
=(-
,
)•(0,
)=
.
故选:D.

在三角形ABC中,∠C=90°,AB=2,AC=1,
∴CB=
| AB2-AC2 |
| 3 |
∴C(0,0),A(1,0),B(0,
| 3 |
∵
| AD |
| 3 |
| 2 |
| AB |
| AD |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
3
| ||
| 2 |
∴
| CD |
| CA |
| AD |
| 3 |
| 2 |
3
| ||
| 2 |
| 1 |
| 2 |
3
| ||
| 2 |
∴
| CD |
| CB |
| 1 |
| 2 |
3
| ||
| 2 |
| 3 |
| 9 |
| 2 |
故选:D.
点评:本题考查了向量的坐标运算和数量积运算,属于基础题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
三棱锥P-ABC中中,顶点P中在底面ABC中内的射影为O中,若
(1)三条侧棱与底面所成的角相等,
(2)三条侧棱两两垂直,
(3)三个侧面与底面所成的角相等;
则点O中依次为垂心、内心、外心的条件分别是( )
(1)三条侧棱与底面所成的角相等,
(2)三条侧棱两两垂直,
(3)三个侧面与底面所成的角相等;
则点O中依次为垂心、内心、外心的条件分别是( )
| A、(1)(2)(3) |
| B、(3)(2)(1) |
| C、(2)(1)(3) |
| D、(2)(3)(1) |
已知a=
(
cosx-sinx)dx,则二项式(x2+
)5展开式中第三项的系数为( )
| ∫ | π 0 |
| 3 |
| a |
| x |
| A、80 | B、-80 |
| C、-40 | D、40 |
若等比数列{an}满足2a4=a6-a5,则q=( )
| A、-1或2 | B、1或-2 |
| C、0 | D、-1或-2 |
设t是实数,i是虚数单位,且
+
是实数,则t=( )
| t |
| 1+i |
| 1-i |
| 2 |
| A、-1 | B、1 | C、0 | D、2 |

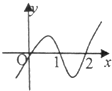
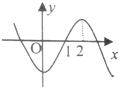
 函数y=f(x)的导函数f′(x)的图象如图所示,则y=f(x)的图象最有可能的是( )
函数y=f(x)的导函数f′(x)的图象如图所示,则y=f(x)的图象最有可能的是( )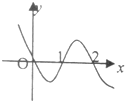

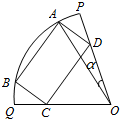 已知OPQ是半径为1,圆心角为2θ(θ为定值)的扇形,A是扇形弧上的动点,四边形ABCD是扇形内的内接矩形,记∠AOP=α(0<α<θ).
已知OPQ是半径为1,圆心角为2θ(θ为定值)的扇形,A是扇形弧上的动点,四边形ABCD是扇形内的内接矩形,记∠AOP=α(0<α<θ).