题目内容
定义:称
为n个正数p1,p2,…,pn的“均倒数”,若数列{an}的前n项的“均倒数”为
,则数列{an}的通项公式为( )
| n |
| p1+p2+…+pn |
| 1 |
| 2n-1 |
| A、2n-1 | B、4n-3 |
| C、4n-1 | D、4n-5 |
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:根据“均倒数”的定义,得到
=
,然后利用an与Sn的关系即可得到结论.
| n |
| a1+a2+…+an |
| 1 |
| 2n-1 |
解答:
解:根据“均倒数”的定义可知,若数列{an}的前n项的“均倒数”为
,
则
=
,即a1+a2+a3+…an=n(2n-1)=2n2-n,
则当n≥2时,a1+a2+a3+…an-1=2(n-1)2-(n-1),
两式相减得an=2n2-n-2(n-1)2+(n-1)=4n-3,
当n=1时,a1=2-1=1,满足,an=4n-3,
故数列{an}的通项公式为an=4n-3,
故选:B
| 1 |
| 2n-1 |
则
| n |
| a1+a2+…+an |
| 1 |
| 2n-1 |
则当n≥2时,a1+a2+a3+…an-1=2(n-1)2-(n-1),
两式相减得an=2n2-n-2(n-1)2+(n-1)=4n-3,
当n=1时,a1=2-1=1,满足,an=4n-3,
故数列{an}的通项公式为an=4n-3,
故选:B
点评:本题主要考查数列通项公式的求解,利用an与Sn的关系是解决本题的关键.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案
相关题目
三棱锥P-ABC中中,顶点P中在底面ABC中内的射影为O中,若
(1)三条侧棱与底面所成的角相等,
(2)三条侧棱两两垂直,
(3)三个侧面与底面所成的角相等;
则点O中依次为垂心、内心、外心的条件分别是( )
(1)三条侧棱与底面所成的角相等,
(2)三条侧棱两两垂直,
(3)三个侧面与底面所成的角相等;
则点O中依次为垂心、内心、外心的条件分别是( )
| A、(1)(2)(3) |
| B、(3)(2)(1) |
| C、(2)(1)(3) |
| D、(2)(3)(1) |
设t是实数,i是虚数单位,且
+
是实数,则t=( )
| t |
| 1+i |
| 1-i |
| 2 |
| A、-1 | B、1 | C、0 | D、2 |
已知某个几何体的三视图如图所示,根据图中数据,求这个几何体的体积是( )

A、
| ||
B、
| ||
C、
| ||
| D、2 |
将4名学生分到三个不同的班级,在每个班级至少分到一名学生的条件下,其中甲、乙两名学生不能分到同一个班级的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
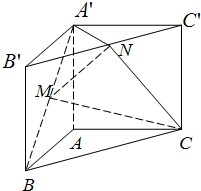 如图,直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=
如图,直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=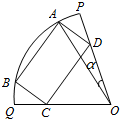 已知OPQ是半径为1,圆心角为2θ(θ为定值)的扇形,A是扇形弧上的动点,四边形ABCD是扇形内的内接矩形,记∠AOP=α(0<α<θ).
已知OPQ是半径为1,圆心角为2θ(θ为定值)的扇形,A是扇形弧上的动点,四边形ABCD是扇形内的内接矩形,记∠AOP=α(0<α<θ). 设四边形ABCD内接于圆O,其对边AD与BC的延长线交于圆O外一点E,自E引一直线平行于AC,交BD延长线于点M,自M引MT切圆O于T点,则MT=ME.
设四边形ABCD内接于圆O,其对边AD与BC的延长线交于圆O外一点E,自E引一直线平行于AC,交BD延长线于点M,自M引MT切圆O于T点,则MT=ME.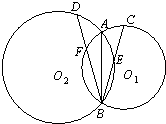 如图,假设两圆O1和O2交于A、B,⊙O1的弦BC交⊙O2于E,⊙O2的弦BD交⊙O1于F,证明:
如图,假设两圆O1和O2交于A、B,⊙O1的弦BC交⊙O2于E,⊙O2的弦BD交⊙O1于F,证明: