题目内容
设等比数列{an}的前n项和为Sn（n∈N*），若
=3，则
= ．
| S6 |
| S3 |
| S9 |
| S6 |
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：根据等比数列的性质得到Sn，S2n-Sn，S3n-S2n成等比列出关系式，又S6：S3=3，表示出S3，代入到列出的关系式中即可求出S9：S6的值．
解答：
解：因为等比数列{an}的前n项和为Sn，则Sn，S2n-Sn，S3n-S2n成等比，（Sn≠0）
所以
=
，
又
=3，即S3=
S6，
所以
=
，
整理得
=
．
故答案为：
．
所以
| S6-S3 |
| S3 |
| S9-S6 |
| S6-S3 |
又
| S6 |
| S3 |
| 1 |
| 3 |
所以
S6-
| ||
|
| S9-S6 | ||
S6-
|
整理得
| S9 |
| S6 |
| 7 |
| 3 |
故答案为：
| 7 |
| 3 |
点评：此题考查学生灵活运用等比数列的性质化简求值，是一道基础题．解本题的关键是根据等比数列的性质得到Sn，S2n-Sn，S3n-S2n成等比．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
相关题目
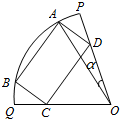已知OPQ是半径为1，圆心角为2θ（θ为定值）的扇形，A是扇形弧上的动点，四边形ABCD是扇形内的内接矩形，记∠AOP=α（0＜α＜θ）．
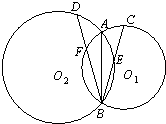如图，假设两圆O1和O2交于A、B，⊙O1的弦BC交⊙O2于E，⊙O2的弦BD交⊙O1于F，证明：
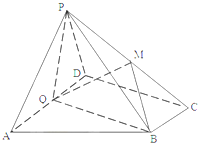如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，Q为AD中点，M是棱PC上的点，PD=PA=2，BC=