题目内容
11．若互不相等的实数a、b、c成等差数列，且c，a，b成等比数列，a+3b+c=10，求a的值．分析 设a=b-d，c=b+d，由题设根据等差数列、等比数列的性质，列出方程组，能求出结果．
解答 解：∵由互不相等的实数a，b，c成等差数列，
∴可设a=b-d，c=b+d，
由题设得：$\left\{\begin{array}{l}{b-d+3b+b+d=10}\\{（b-d）^{2}=b（b+d）}\end{array}\right.$，
解方程组得$\left\{\begin{array}{l}{b=2}\\{d=6}\end{array}\right.$，或$\left\{\begin{array}{l}{b=2}\\{d=0}\end{array}\right.$，
∵d≠0，
∴b=2，d=6，
∴a=b-d=-4，
故a的值为-4．
点评 本题考查等差数列、等比数列等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，是基础题．
练习册系列答案
相关题目
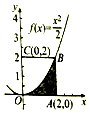如图，利用随机模拟的方法可以估计图中由曲线$y=\frac{x^2}{2}$与两直线x=2及y=0所围成的阴影部分的面积S：
3．已知全集U=Z，A={x|x2-x-2＜0，x∈Z}，B={-1，0，1，2}，则（∁UA）∩B等于（ ）
| A． | {-1，2} | B． | {-1，0} | C． | {0，1} | D． | {1，2} |