题目内容
1.甲、乙两位学生参加数学竞赛培训,在培训期间他们参加的5次预赛成绩记录如下:甲:82,82,79,95,87
乙:95,75,80,90,85
(1)用茎叶图表示这两组数据;
(2)求甲、乙两人的成绩的平均数与方差;
(3)若现要从中选派一人参加数学竞赛,你认为选派哪位学生参加合适说明理由?
分析 (1)以十位数为茎,以个位数为叶,能作出茎叶图.
(2)由题意能求出甲、乙的成绩的平均数与方差.
(3)甲乙的平均分一样,证明平均成绩一样,但是甲的方差小于乙的方差,则证明甲的成绩更稳定,由此得到选派甲学生参加合适.
解答 解:(1)以十位数为茎,以个位数为叶,作出茎叶图如右图所示.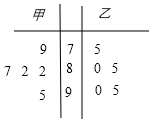
(2)甲的成绩的平均数$\overline{{x}_{甲}}$=$\frac{1}{5}$(82+82+79+95+87)=85,
乙的成绩的平均数$\overline{{x}_{乙}}$=$\frac{1}{5}$(75+95+80+90+85)=85,
甲的方差${{S}_{甲}}^{2}$=$\frac{1}{5}$[(82-85)2+(82-85)2+(79-85)2+(95-85)2+(87-85)2]=31.6,
乙的方差${{S}_{乙}}^{2}$=$\frac{1}{5}$[(75-85)2+(95-85)2+(80-85)2+(90-85)2+(85-85)2]=50.
(3)派甲参赛比较合理.
理由是甲乙的平均分一样,证明平均成绩一样,
但是甲的方差小于乙的方差,则证明甲的成绩更稳定.
点评 本题考查茎叶图、平均数、方差等基础知识,考查推理论证能力、运算求解能力、数据处理能力,考查化归与转化思想、函数与方程思想、数形结合思想,考查创新意识、应用意识,是基础题.

练习册系列答案
相关题目
12.已知数列{an}的前n项和为Sn,a1=1,2Sn=an+1,则an+1=( )
| A. | 2n-1 | B. | 2n-1 | C. | 2×3n-1. | D. | $\frac{1}{2}({{3^n}-1})$ |
16.设函数$f(x)=sin(x+\frac{7π}{4})+cos(x-\frac{3π}{4})$则( )
| A. | y=f(x)的最小正周期是π,其图象关于$x=-\frac{π}{4}$对称 | |
| B. | y=f(x)的最小正周期是2π,其图象关于$x=\frac{π}{2}$对称 | |
| C. | y=f(x)的最小正周期是π,其图象关于$x=\frac{π}{2}$对称 | |
| D. | y=f(x)的最小正周期是2π,其图象关于$x=-\frac{π}{4}$对称 |
13.已知角θ在第二象限,且$|{sin\frac{θ}{2}}|=-sin\frac{θ}{2}$,则 $\frac{θ}{2}$在( )
| A. | 第一象限或第三象限 | B. | 第二象限或第四象限 | ||
| C. | 第三象限 | D. | 第四象限 |
11.已知角α的始边为x轴的正半轴,点(1,3)是角α终边上的一点,则tanα=( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | 3 |
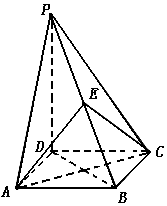 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.