题目内容
19.数列{an}满足${a_1}+2a_2^{\;}+{2^2}{a_3}+…+{2^{n-1}}{a_n}={n^2}$,则an=$\frac{2n-1}{{2}^{n-1}}$.分析 根据题干条件求出a1+2a2+22a3+…+2n-2an-1=(n-1)2,与题干等式相减即可求出数列{an}的表达式.
解答 解:∵a1+2a2+22a3+…+2n-1an=n2…①,
∴a1+2a2+22a3+…+2n-2an-1=(n-1)2…②,
①-②得2n-1an=2n-1,
∴an=$\frac{2n-1}{{2}^{n-1}}$,
当n=1时,a1=$\frac{1}{1}$=1=12,
∴an=$\frac{2n-1}{{2}^{n-1}}$,
故答案为:$\frac{2n-1}{{{2^{n-1}}}}$
点评 本题主要考查数列递推式的知识点,解答本题的关键是求出a1+2a2+22a3+…+2n-2an-1=(n-1)2,此题比较简单.

练习册系列答案
相关题目
7.已知p:?x∈[1,2],x2-a≥0,q:方程x2+2ax+2-a=0有实数解,若p且q为真命题,则实数a的取值范围是( )
| A. | a≤-2或a=1 | B. | a≤2或1≤a≤2 | C. | a≥1 | D. | -2≤a≤1 |
14.i为虚数单位,复数$\frac{1+3i}{1-i}$=( )
| A. | -1+2i | B. | 1-2i | C. | -1-2i | D. | 1+2i |
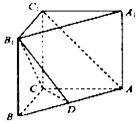 如图,直三棱柱ABC-A1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点D在线段AB上.
如图,直三棱柱ABC-A1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点D在线段AB上.