题目内容

两灯塔A，B与海洋观测站C之间的距离都等于2km，灯塔A在C北偏东45°处，灯塔B在C南偏东15°处，则A，B之间的距离为
 
．
考点：余弦定理
专题：三角函数的求值
分析：根据题意画出图形，如图所示，在三角形ABC值，利用余弦定理列出关系式，将AC，BC，以及cos∠ACB的值代入即可求出AB的长．
解答： 解：根据题意画出图形，如图所示，CA=CB=2km，∠ACB=120°，
在△ABC中，由余弦定理得：AB2=AC2+BC2-2AC•BC•cos∠ACB=4+4+4=12，
则AB=2
3
km．
故答案为：2
3
km
点评：此题考查了余弦定理，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
等差数列{an}的前n项和为Sn，且S2=6，a1=4，则公差d等于（　　）
A、3B、2C、1D、-2
设关于x的一元二次方程ax2-2bx+a=0（a，b∈R）
（Ⅰ）若a是集合{1，2，3}中任取一个元素，b是从集合{1，2，3}中任取一个元素，求上述方程有两个不相等实数根的概率．
（Ⅱ）若a是从区间（0，3）任取的一个实数，b是从区间（0，2）任取的一个实数，求上述方程没有实数根的概率．
已知f（x）=（x-1）2，g（x）=4（x-1）．数列{an}满足a1=2，（an+1-an）g（an）+f（an）=0．
（1）用an表示an+1；
（2）求证：{an-1}是等比数列
（3）（文科），若数列{an}的前n项和为Sn，试求n的最小值，使得Sn＞n+3恒成立．
（理科）若bn=3f（an）-g（an+1），求数列{bn}的最大项和最小项．
（1）若实数x，y满足：
x-y+1≤0
x＞0
，求
y
x
的范围；
（2）设正数x，y满足x+2y=1，求
1
x
+
1
y
的最小值；
（3）已知x＜
5
4
，求y=4x+
1
4x-5
-2的最大值．
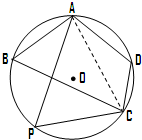市某棚户区改造建筑用地平面示意图如图所示．经规划调研确定，棚改规划建筑用地区域是半径为R的圆面．该圆面的内接四边形ABCD是原棚户建筑用地，测量可知边界AB=AD=4万米，BC=6万米，CD=2万米．
（Ⅰ）求原棚户区建筑用地ABCD中对角A，C两点的距离；
（Ⅱ）请计算出原棚户区建筑用地ABCD的面积及圆的半径R；
（Ⅲ）因地理条件的限制，边界AD，DC不能变更，而边界AB，BC可以调整，为了提高棚户区改造建筑用地的利用率，请在圆弧ABC上设计一点P，使得棚户区改造的新建筑用地APCD的面积最大，并求最大值．
已知数列{an}是一个等差数列，且a2=1，a6=-5．
（1）求{an}的通项an和前n项和Sn．
（2）设cn=
5-an
2
，bn=2 cn，证明数列{bn}是等比数列．
（3）设cn=5-an，bn=
1
cn2-1
（n∈N*），求数列{bn}的前n项和Tn．
已知函数f（x）=lnx-kx+1．求：
（1）求函数f（x）的单调区间；
（2）若f（x）≤0恒成立，试确定实数k的取值范围．
已知函数f（x）=log2（-4x+5•2x+1-16）．
（1）求f（x）的定义域；
（2）求f（x）在区间[2，log27]上的值域．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网