题目内容
 选修4.1:几何证明选讲
选修4.1:几何证明选讲如图所示,己知D为△ABC的BC边上一点,⊙O1经过点B,D,交AB于另一点E⊙O2经过点C,D,交AC于另一点F,⊙O1与⊙O2的另一交点为G
(Ⅰ)求证:A、E、G、F四点共圆
(Ⅱ)若AG切⊙O2于G,求证:∠AEF=∠ACG.
考点:圆內接多边形的性质与判定,圆的切线的性质定理的证明
专题:选作题,立体几何
分析:(Ⅰ)连接GD,由圆内接四边形的性质,可得∠AEG=∠BDG,∠AFG=∠CDG,从而可得∠AEG+∠AFG=180°,即可证明A、E、G、F四点共圆;
(Ⅱ)A、E、G、F四点共圆,可得∠AEF=∠AGF,由AG切⊙O2于G,可得∠AGF=∠ACG,从而可得结论.
(Ⅱ)A、E、G、F四点共圆,可得∠AEF=∠AGF,由AG切⊙O2于G,可得∠AGF=∠ACG,从而可得结论.
解答:
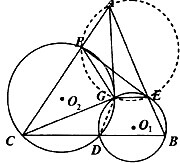 证明:(Ⅰ)连接GD.
证明:(Ⅰ)连接GD.
∵四边形BDGE,CDGF是圆内接四边形,
∴∠AEG=∠BDG,∠AFG=∠CDG
∵∠BDG+∠CDG=180°,
∴∠AEG+∠AFG=180°,
∴A、E、G、F四点共圆;
(Ⅱ)∵A、E、G、F四点共圆,
∴∠AEF=∠AGF,
∵AG切⊙O2于G,
∴∠AGF=∠ACG,
∴∠AEF=∠ACG.
 证明:(Ⅰ)连接GD.
证明:(Ⅰ)连接GD.∵四边形BDGE,CDGF是圆内接四边形,
∴∠AEG=∠BDG,∠AFG=∠CDG
∵∠BDG+∠CDG=180°,
∴∠AEG+∠AFG=180°,
∴A、E、G、F四点共圆;
(Ⅱ)∵A、E、G、F四点共圆,
∴∠AEF=∠AGF,
∵AG切⊙O2于G,
∴∠AGF=∠ACG,
∴∠AEF=∠ACG.
点评:本题以三角形内角和与圆内接四边形为例,考查了与圆有关的角相等和角互补的证明,属于基础题.

练习册系列答案
相关题目
(文科)tan21°+tan24°+tan21°tan24°=( )
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
已知
=
,则tanα的值是( )
| sinα-cosα |
| 2sinα+3cosα |
| 1 |
| 5 |
A、±
| ||
B、
| ||
C、-
| ||
| D、无法确定 |