题目内容
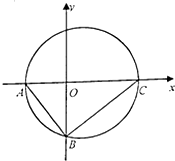 如图所示,在Rt△ABC中,已知A(-2,0),直角顶点B(0,-2
如图所示,在Rt△ABC中,已知A(-2,0),直角顶点B(0,-2| 2 |
(Ⅰ)求Rt△ABC外接圆的方程;
(Ⅱ)求过点(-4,0)且与Rt△ABC外接圆相切的直线的方程.
考点:圆的切线方程
专题:直线与圆
分析:(Ⅰ)设点C(a,0),由BA⊥BC,KBA•KBC=-1,求得a的值,可得所求的圆的圆心、半径,可得要求圆的方程.
(Ⅱ)设要求直线的方程为y=k(x+4),根据圆心到直线的距离等于半径,即d=
=3,求得k的值,可得要求的直线的方程.
(Ⅱ)设要求直线的方程为y=k(x+4),根据圆心到直线的距离等于半径,即d=
| |5k| | ||
|
解答:
解:(Ⅰ)设点C(a,0),由BA⊥BC,可得 KBA•KBC=
•
=-1,∴a=4,
故所求的圆的圆心为AC的中点(1,0)、半径为
AC=3,
故要求Rt△ABC外接圆的方程为(x-1)2+y2=9.
(Ⅱ)由题意可得,要求的直线的斜率一定存在,设要求直线的方程为y=k(x+4),
即 kx-y+4k=0,当直线和圆相切时,圆心到直线的距离等于半径,
故有 d=
=3,求得k=±
,
故要求的直线的方程为 3x-4y+12=0,或 3x+4y+12=0.
-2
| ||
| 2 |
2
| ||
| a |
故所求的圆的圆心为AC的中点(1,0)、半径为
| 1 |
| 2 |
故要求Rt△ABC外接圆的方程为(x-1)2+y2=9.
(Ⅱ)由题意可得,要求的直线的斜率一定存在,设要求直线的方程为y=k(x+4),
即 kx-y+4k=0,当直线和圆相切时,圆心到直线的距离等于半径,
故有 d=
| |5k| | ||
|
| 3 |
| 4 |
故要求的直线的方程为 3x-4y+12=0,或 3x+4y+12=0.
点评:本题主要考查两条直线垂直的性质,求圆的标准方程,用待定系数法求直线的方程,点到直线的距离公式的应用,属于基础题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
在等比数列{an}中,若a1=3,a2=9,则数列{an}的前4项和为( )
| A、81 | B、120 |
| C、168 | D、192 |
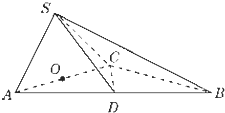 已知三棱锥S-ABC中,平面ASC⊥平面ABC,O、D分别为AC、AB的中点,AS=CS=CD=AD=
已知三棱锥S-ABC中,平面ASC⊥平面ABC,O、D分别为AC、AB的中点,AS=CS=CD=AD=