题目内容
12．设数列{an}的前n项和为Sn，令Tn=$\frac{{S}_{1}+{S}_{2}+…+{S}_{n}}{n}$，称Tn为数列a1，a2，…，an的“理想数”，已知数列a1，a2，…，a500的“理想数”为2004，求数列15，a1，a2，…，a500的“理想数”．分析 由新定义可知S1+S2+S3+…+S500=2004×500，所以新数列中对应的理想数的分子为15×501+2004×500．代入新定义计算即可求出．
解答 解：∵数列a1，a2，…，a500的“理想数”为2004，∴S1+S2+S3+…+S500=2004×500．
设数列15，a1，a2，…，a500的前n项和为An，则An=Sn-1+15．
∴A1+A2+A3+…+A501=15+（S1+15）+（S2+15）+…+（S500+15）=15×501+2004×500．
∴数列15，a1，a2，…，a500的“理想数”为$\frac{15×501+2004×500}{501}$=15+2000=2015．
点评 本题考查了对新定义的理解和数列求和，属于中档题．
练习册系列答案
相关题目
2．
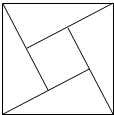如图，四个全等的直角三角形围成一个大正方形和一个小正方形，若直角三角形较长的直角边为4，小正方形的面积为9．现向大正方形内随机撒一枚幸运小星星，则小星星落在小正方形内的概率为（ ）
如图，四个全等的直角三角形围成一个大正方形和一个小正方形，若直角三角形较长的直角边为4，小正方形的面积为9．现向大正方形内随机撒一枚幸运小星星，则小星星落在小正方形内的概率为（ ）| A． | $\frac{8}{17}$ | B． | $\frac{9}{17}$ | C． | $\frac{10}{17}$ | D． | $\frac{11}{17}$ |
4．已知sin（$\frac{π}{3}$+a）=$\frac{12}{13}$，a∈（$\frac{π}{6}$，$\frac{2π}{3}$），则cosα的值为 （ ）
| A． | $\frac{12\sqrt{3}-5}{13}$ | B． | $\frac{12\sqrt{3}-5}{26}$ | C． | $\frac{12\sqrt{3}+5}{13}$ | D． | $\frac{12\sqrt{3}+5}{26}$ |