题目内容
1.设点M在x轴上,若M到直线x-$\sqrt{3}$y+7=0和12x-5y+40=0的距离相等,则M点的坐标是(1,0)或(-$\frac{91}{37}$,0).分析 设M(a,0),由点到直线距离公式得$\frac{|a+7|}{\sqrt{1+3}}=\frac{|12a+40|}{\sqrt{144+25}}$,由此能求出M点坐标.
解答 解:∵点M在x轴上,∴设M(a,0),
∵M到直线x-$\sqrt{3}$y+7=0和12x-5y+40=0的距离相等,
∴$\frac{|a+7|}{\sqrt{1+3}}=\frac{|12a+40|}{\sqrt{144+25}}$,
解得a=1或a=-$\frac{91}{37}$,
∴M(1,0)或M(-$\frac{91}{37}$,0).
故答案为:(1,0)或(-$\frac{91}{37}$,0).
点评 本题考查点的坐标的求法,是基础题,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
相关题目
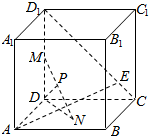 已知棱长为3的正方体ABCD-A1B1C1D1中,长为2的线段MN的一端点M在DD1上运动,另一个端点N在底面ABCD上运动,动点E在线段CD1上,则MN中点P到线段AE距离的最小值为$\sqrt{3}-1$.
已知棱长为3的正方体ABCD-A1B1C1D1中,长为2的线段MN的一端点M在DD1上运动,另一个端点N在底面ABCD上运动,动点E在线段CD1上,则MN中点P到线段AE距离的最小值为$\sqrt{3}-1$.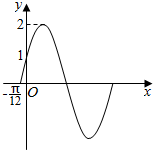 能否由下列图象唯一地确定函数y=Asin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的解析式?如果能.求出它的解析式;如果不能,请你加一个条件.确定它的解析式.
能否由下列图象唯一地确定函数y=Asin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的解析式?如果能.求出它的解析式;如果不能,请你加一个条件.确定它的解析式.