题目内容
20.在△ABC中,a,b,c分别为内角A、B、C的对边,且2asinA=(2b+c)sinB+(2c+b)sinC,则A的大小是120°.分析 根据正弦定理,设 a=2RsinA,b=2RsinB,c=2RsinC,把sinA,sinB,sinC代入2asinA=(2b+c)sinB+(2c+b)sinC求出a2=b2+c2+bc再与余弦定理联立方程,可求出cosA的值,进而求出A的值.
解答 解:由正弦定理可得:a=2RsinA,b=2RsinB,c=2RsinC,
∵2asinA=(2a+c)sinB+(2C+b)sinC,
方程两边同乘以2R,
∴2a2=(2b+c)b+(2c+b)c,
整理得a2=b2+c2+bc,
∵由余弦定理得a2=b2+c2-2bccosA,
故cosA=-$\frac{1}{2}$,A=120°.
故答案为:120°.
点评 本题主要考查了正弦定理与余弦函数的应用.主要用于解决三角形中边、角问题,故应熟练掌握,考查计算能力.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
15.若复数z=$\frac{a+3i}{i}$+a在复平面上对应的点在第二象限,则实数a可以是( )
| A. | -4 | B. | -3 | C. | 1 | D. | 2 |
5.在△ABC中,a=3,$b=\sqrt{5}$,A=60°,则cosB=( )
| A. | $±\frac{{\sqrt{15}}}{6}$ | B. | $\frac{{\sqrt{15}}}{6}$ | C. | $±\frac{{\sqrt{21}}}{6}$ | D. | $\frac{{\sqrt{21}}}{6}$ |
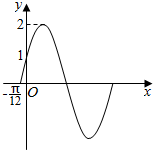 能否由下列图象唯一地确定函数y=Asin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的解析式?如果能.求出它的解析式;如果不能,请你加一个条件.确定它的解析式.
能否由下列图象唯一地确定函数y=Asin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的解析式?如果能.求出它的解析式;如果不能,请你加一个条件.确定它的解析式.