题目内容
2．
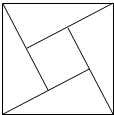如图，四个全等的直角三角形围成一个大正方形和一个小正方形，若直角三角形较长的直角边为4，小正方形的面积为9．现向大正方形内随机撒一枚幸运小星星，则小星星落在小正方形内的概率为（ ）| A． | $\frac{8}{17}$ | B． | $\frac{9}{17}$ | C． | $\frac{10}{17}$ | D． | $\frac{11}{17}$ |
分析 根据几何概型概率的求法，飞镖扎在小正方形内的概率为小正方形内与大正方形的面积比，根据题意，可得小正方形的面积与大正方形的面积，进而可得答案．
解答 解：根据题意，小正方形的面积为9，则小正方形的边长是3，
又直角三角形较长的直角边为4，
得出四个全等的直角三角直角边分别是4和1，
∴大正方形的面积为17，
故飞镖扎在小正方形内的概率为$\frac{9}{17}$．
故选：B．
点评 用到的知识点为：概率=相应的面积与总面积之比；难点是得到正方形的边长．
练习册系列答案
相关题目
12．已知复数z（1+i）=2i，则复数z=（ ）
| A． | 1+i | B． | 1-i | C． | $\frac{1}{2}$+$\frac{1}{2}$i | D． | $\frac{1}{2}$-$\frac{1}{2}$i |
17．已知m、n是两条不同直线，α、β是两个不同平面，给出下列命题，其中正确的是（ ）
| A． | 若α∩β=m，n?α，n⊥m，则α⊥β | B． | 若m∥β，n∥β，m、n?α，则α∥β | ||
| C． | 若m⊥α，n⊥β，m⊥n，则α⊥β | D． | 若m∥α，n∥β，m∥n，则α∥β |
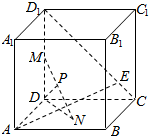已知棱长为3的正方体ABCD-A1B1C1D1中，长为2的线段MN的一端点M在DD1上运动，另一个端点N在底面ABCD上运动，动点E在线段CD1上，则MN中点P到线段AE距离的最小值为$\sqrt{3}-1$．