Question

19．某校为了解甲、乙两班学生的学业水平，从两班中各随机抽取20人参加学业水平等级考试，得到学生的学业成绩茎叶图如下：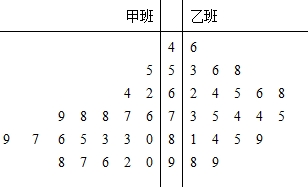

（Ⅰ）通过茎叶图比较甲、乙两班学生的学业成绩平均值$\overline{X}$_甲与${\overline X_乙}$及方差$s_甲^2$与$s_乙^2$的大小；（只需写出结论）
（Ⅱ）根据学生的学业成绩，将学业水平分为三个等级：

学业成绩	低于70分	70分到89分	不低于90分
学业水平	一般	良好	优秀

根据所给数据，频率可以视为相应的概率．
（ⅰ）从甲、乙两班中各随机抽取1人，记事件C：“抽到的甲班学生的学业水平等级高于乙班学生的学业水平等级”，求C发生的概率；
（ⅱ）从甲班中随机抽取2人，记X为学业水平优秀的人数，求X的分布列和数学期望．

Answer 1

分析 （Ⅰ）由茎叶图能得到${\overline X_甲}＞{\overline X_乙}$，$s_甲^2＜s_乙^2$．
（Ⅱ）（i）记A₁、A₂、A₃分别表示事件：甲班学生学业水平等级为一般、良好、优秀；记B₁、B₂、B₃分别表示事件：乙班学生学业水平等级为一般、良好、优秀，由P（C）=P（A₂B₁）+P（A₃B₁）+P（A₃B₂），能求出C发生的概率．
（ii）从甲班随机抽取1人，其学业水平优秀的概率为$\frac{1}{4}$，则X=0，1，2，X～B（2，$\frac{1}{4}$），由此能求出X的分布列和数学期望．

解答 解：（Ⅰ）由茎叶图得${\overline X_甲}＞{\overline X_乙}$，$s_甲^2＜s_乙^2$．
（Ⅱ）（i）记A₁、A₂、A₃分别表示事件：甲班学生学业水平等级为一般、良好、优秀；
记B₁、B₂、B₃分别表示事件：乙班学生学业水平等级为一般、良好、优秀，
则P（C）=P（A₂B₁）+P（A₃B₁）+P（A₃B₂）
=P（A₂）P（B₁）+P（A₃）P（B₁）+P（A₃）P（B₂）
=$\frac{12}{20}×\frac{9}{20}+\frac{5}{20}×\frac{9}{20}+\frac{5}{20}×\frac{9}{20}$=$\frac{99}{200}$，
（ii）从甲班随机抽取1人，其学业水平优秀的概率为$\frac{1}{4}$，
则X=0，1，2，X～B（2，$\frac{1}{4}$），
$P（X=0）=C_2^0{（\frac{3}{4}）^2}=\frac{9}{16}$，
$P（X=1）=C_2^1\frac{1}{4}•\frac{3}{4}=\frac{6}{16}=\frac{3}{8}$，
$P（X=2）=C_2^2{（\frac{1}{4}）^2}=\frac{1}{16}$，
则X的分布列为：

X	0	1	2
P	$\frac{9}{16}$	$\frac{3}{8}$	$\frac{1}{16}$

$EX=np=2×\frac{1}{4}=2$（或$EX=0×\frac{9}{16}+1×\frac{3}{8}+2×\frac{1}{16}=2$）．

点评 本题考查概率的求法，考查离散型随机变量的分布列和数学期望的求法，是中档题，解题时要认真审题，注意二项分布的性质的合理运用．