题目内容
9.已知等边△ABC的边长为8$\sqrt{3}$,且三个顶点都在抛物线y2=4mx(m>0)上,抛物线的准线与x轴交于点M,自M引直线交抛物线于P、Q两个不同的点,设$\overrightarrow{MP}$=λ$\overrightarrow{MQ}$(1)求抛物线的方程;
(2)若λ∈[$\frac{1}{2}$,1),求|PQ|的取值范围.
分析 (1)由题意,点(12,4$\sqrt{3}$)在抛物线y2=4mx(m>0)上,求出m,即可求抛物线的方程;
(2)利用$\overrightarrow{MP}$=λ$\overrightarrow{MQ}$,M(-1,0),求出P,Q的坐标,表示出|PQ|,利用λ∈[$\frac{1}{2}$,1),求|PQ|的取值范围.
解答 解:(1)由题意,点(12,4$\sqrt{3}$)在抛物线y2=4mx(m>0)上,
∴48=48m,
∴m=1,
∴抛物线的方程为y2=4x;
(2)设P(x1,y1)、Q(x2,y2),
∵$\overrightarrow{MP}$=λ$\overrightarrow{MQ}$,M(-1,0),
∴(x1+1,y1)=λ(x2+1,y2),
∴y1=λy2,x1+1=λ(x2+1),
∴x1=λ2x2,
∴λ2x2+1=λ(x2+1),
∴x2=$\frac{1}{λ}$,x1=λ,
∴取P(λ,2$\sqrt{λ}$),Q($\frac{1}{λ}$,$\frac{2}{\sqrt{λ}}$),
∴|PQ|2=(λ-$\frac{1}{λ}$)2+(2$\sqrt{λ}$-$\frac{2}{\sqrt{λ}}$)2=λ2+$\frac{1}{{λ}^{2}}$+4(λ+$\frac{1}{λ}$)-10,
设λ+$\frac{1}{λ}$=t,t∈(2,$\frac{5}{2}$],∴|PQ|2=t2+4t-12=(t+2)2-16∈(0,$\frac{17}{4}$]
∴|PQ|∈(0,$\frac{\sqrt{17}}{2}$].
点评 本题考查抛物线方程,考查向量知识的运用,考查学生分析解决问题的能力,确定P,Q的坐标是关键.

练习册系列答案
相关题目
19.某校为了解甲、乙两班学生的学业水平,从两班中各随机抽取20人参加学业水平等级考试,得到学生的学业成绩茎叶图如下:
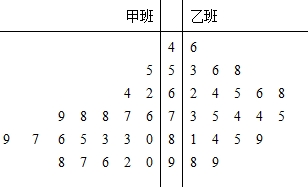
(Ⅰ)通过茎叶图比较甲、乙两班学生的学业成绩平均值$\overline{X}$甲与${\overline X_乙}$及方差$s_甲^2$与$s_乙^2$的大小;(只需写出结论)
(Ⅱ)根据学生的学业成绩,将学业水平分为三个等级:
根据所给数据,频率可以视为相应的概率.
(ⅰ)从甲、乙两班中各随机抽取1人,记事件C:“抽到的甲班学生的学业水平等级高于乙班学生的学业水平等级”,求C发生的概率;
(ⅱ)从甲班中随机抽取2人,记X为学业水平优秀的人数,求X的分布列和数学期望.

(Ⅰ)通过茎叶图比较甲、乙两班学生的学业成绩平均值$\overline{X}$甲与${\overline X_乙}$及方差$s_甲^2$与$s_乙^2$的大小;(只需写出结论)
(Ⅱ)根据学生的学业成绩,将学业水平分为三个等级:
| 学业成绩 | 低于70分 | 70分到89分 | 不低于90分 |
| 学业水平 | 一般 | 良好 | 优秀 |
(ⅰ)从甲、乙两班中各随机抽取1人,记事件C:“抽到的甲班学生的学业水平等级高于乙班学生的学业水平等级”,求C发生的概率;
(ⅱ)从甲班中随机抽取2人,记X为学业水平优秀的人数,求X的分布列和数学期望.
17.已知函数f(x)=sinωx+cosωx(ω>0)在($\frac{π}{2}$,π)上单调递减,则ω的取值范围是( )
| A. | [$\frac{1}{2}$,$\frac{5}{4}$] | B. | [$\frac{1}{2}$,$\frac{3}{4}$] | C. | (0,$\frac{1}{2}$] | D. | (0,2] |
1.已知随机变量X的分布列为:.
若Y=2X-3,则P(1<Y≤5)=0.6.
| X | 1 | 2 | 3 | 4 | 5 |
| P | 0.1 | 0.2 | 0.4 | 0.2 | 0.1 |
 如图,D、E、F分别是△ABC的边BC、CA、AB上的点,AD与EF相交于G,已知CD=2DB,AF=4FB,AG=mAD,AE=tAC.
如图,D、E、F分别是△ABC的边BC、CA、AB上的点,AD与EF相交于G,已知CD=2DB,AF=4FB,AG=mAD,AE=tAC.