题目内容
14.已知寒素f(x)=3x2-2mx-1(m∈R).(1)若函数f(x)在区间(1,2)上是单调函数,求实数m的取值范围;
(2)若函数f(x)在区间[0,1]上的最小值为g(m),求g(m)的表达式;
(3)已知h(x)为奇函数,当x≥0时,h(x)=f(x)+2mx+1,若h(2x-3)≤h(x+cosθ)对θ∈R恒成立,求实数x的取值范围.
分析 (1)由f(x)在(1,2)上单调可知$\frac{m}{3}$≤1或$\frac{m}{3}$≥2,解出m的范围;
(2)根据对称轴与区间[0,1]的关系分三种情况讨论f(x)在[0,1]上的单调性,求出f(x)的最小值;
(3)求出h(x)的解析式并判断好h(x)的单调性,利用单调性得出2x-3与x+cosθ的大小关系,解不等式得出x的范围.
解答 解:(1)f(x)的对称轴为x=$\frac{m}{3}$,
∵函数f(x)在区间(1,2)上是单调函数,∴$\frac{m}{3}$≤1或$\frac{m}{3}$≥2,解得m≤3或m≥6.
∴m的取值范围是(-∞,3]∪[6,+∞).
(2)①若$\frac{m}{3}$≤0,即m≤0时,f(x)在[0,1]上是增函数,∴g(m)=f(0)=-1.
②若$\frac{m}{3}$≥1,即m≥3时,f(x)在[0,1]上是减函数,∴g(m)=f(1)=2-2m.
③若0<$\frac{m}{3}$<1,即0<m<3时,f(x)在[0,1]上先减后增,∴g(m)=f($\frac{m}{3}$)=-$\frac{{m}^{2}}{3}$-1.
综上,g(m)=$\left\{\begin{array}{l}{-1,m≤0}\\{-\frac{{m}^{2}}{3}-1,0<m<3}\\{2-2m,m≥3}\end{array}\right.$.
(3)当x≥0时,h(x)=3x2,
设x<0,则-x>0,∴h(-x)=3x2,
∵h(x)为奇函数,∴h(x)=-h(-x)=-3x2,
∴h(x)=$\left\{\begin{array}{l}{3{x}^{2},x≥0}\\{-3{x}^{2},x<0}\end{array}\right.$.∴h(x)在R上是增函数.
∵h(2x-3)≤h(x+cosθ)对θ∈R恒成立,
∴2x-3≤x+cosθ对θ∈R恒成立.∴x≤3+cosθ对θ∈R恒成立.
∵-1≤cosθ≤1,∴x≤2.
∴实数x的取值范围是(-∞,2].
点评 本题考查了二次函数的单调性,最小值以及函数恒成立问题,对对称轴与区间的关系进行讨论是解题关键,属于中档题.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案| A. | -1 | B. | 1 | C. | 2 | D. | $\sqrt{2}$ |
| 广告费x(万元) | 3 | 4 | 5 | 6 |
| 销售额y(万元) | 25 | 30 | 40 | 45 |
| A. | 72.5 | B. | 73.5 | C. | 74.5 | D. | 75.5 |
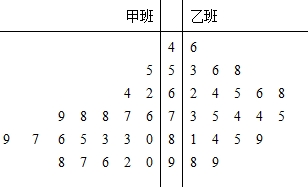
(Ⅰ)通过茎叶图比较甲、乙两班学生的学业成绩平均值$\overline{X}$甲与${\overline X_乙}$及方差$s_甲^2$与$s_乙^2$的大小;(只需写出结论)
(Ⅱ)根据学生的学业成绩,将学业水平分为三个等级:
| 学业成绩 | 低于70分 | 70分到89分 | 不低于90分 |
| 学业水平 | 一般 | 良好 | 优秀 |
(ⅰ)从甲、乙两班中各随机抽取1人,记事件C:“抽到的甲班学生的学业水平等级高于乙班学生的学业水平等级”,求C发生的概率;
(ⅱ)从甲班中随机抽取2人,记X为学业水平优秀的人数,求X的分布列和数学期望.
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |