题目内容
8.△ABC中,角A、B、C所对的边为a、b、c,且角A=60°,a=2,则△ABC的周长的最大值为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 根据余弦定理,算出(b+c)2=4+3bc,再利用基本不等式bc≤[$\frac{1}{2}$(b+c)]2,加以计算,可得b+c≤4,即可得到△ABC周长的最大值.
解答 解:∵在△ABC中,A=60°,a=2,
∴由余弦定理,得a2=b2+c2-2bccosA,
即4=b2+c2-2bccos60°,化简得(b+c)2=4+3bc,
∵bc≤[$\frac{1}{2}$(b+c)]2,
∴(b+c)2≤4+$\frac{3}{4}$(b+c)2,解得(b+c)2≤16,
由此可得b+c≤4,△ABC周长AB+AC+BC≤6.
即当且仅当b=c=2时,△ABC周长的最大值为6.
故选:C.
点评 本题给出三角形的一边和它的对角,求周长的最大值.着重考查了用余弦定理解三角形和基本不等式求最值等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.用与球心距离为4的平面去截球所得的截面面积为9π,则球的表面积为( )
| A. | 36π | B. | 64π | C. | 100π | D. | 144π |
19.某校为了解甲、乙两班学生的学业水平,从两班中各随机抽取20人参加学业水平等级考试,得到学生的学业成绩茎叶图如下:
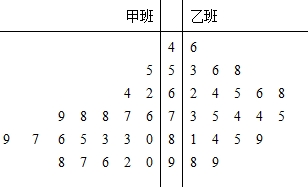
(Ⅰ)通过茎叶图比较甲、乙两班学生的学业成绩平均值$\overline{X}$甲与${\overline X_乙}$及方差$s_甲^2$与$s_乙^2$的大小;(只需写出结论)
(Ⅱ)根据学生的学业成绩,将学业水平分为三个等级:
根据所给数据,频率可以视为相应的概率.
(ⅰ)从甲、乙两班中各随机抽取1人,记事件C:“抽到的甲班学生的学业水平等级高于乙班学生的学业水平等级”,求C发生的概率;
(ⅱ)从甲班中随机抽取2人,记X为学业水平优秀的人数,求X的分布列和数学期望.

(Ⅰ)通过茎叶图比较甲、乙两班学生的学业成绩平均值$\overline{X}$甲与${\overline X_乙}$及方差$s_甲^2$与$s_乙^2$的大小;(只需写出结论)
(Ⅱ)根据学生的学业成绩,将学业水平分为三个等级:
| 学业成绩 | 低于70分 | 70分到89分 | 不低于90分 |
| 学业水平 | 一般 | 良好 | 优秀 |
(ⅰ)从甲、乙两班中各随机抽取1人,记事件C:“抽到的甲班学生的学业水平等级高于乙班学生的学业水平等级”,求C发生的概率;
(ⅱ)从甲班中随机抽取2人,记X为学业水平优秀的人数,求X的分布列和数学期望.
17.已知函数f(x)=sinωx+cosωx(ω>0)在($\frac{π}{2}$,π)上单调递减,则ω的取值范围是( )
| A. | [$\frac{1}{2}$,$\frac{5}{4}$] | B. | [$\frac{1}{2}$,$\frac{3}{4}$] | C. | (0,$\frac{1}{2}$] | D. | (0,2] |