题目内容
给定下列四个命题:
①命题“?x∈R,x2-x>0”的否定是“对?x∈R,x2-x<0”;
②若p:0<x<2是q:a-1<x≤a的必要不充分条件,则a的取值范围是[1,2];
③幂函数f(x)=(m2-m-1)xm2+m-3在x=0处有定义,则实数m的值为2;
④已知向量
=(3,-4),
=(2,1),则向量
在向量
方向上的投影是
.
其中正确命题的序号是 .
①命题“?x∈R,x2-x>0”的否定是“对?x∈R,x2-x<0”;
②若p:0<x<2是q:a-1<x≤a的必要不充分条件,则a的取值范围是[1,2];
③幂函数f(x)=(m2-m-1)xm2+m-3在x=0处有定义,则实数m的值为2;
④已知向量
| a |
| b |
| a |
| b |
| 2 |
| 5 |
其中正确命题的序号是
考点:命题的真假判断与应用
专题:简易逻辑
分析:①命题“?x∈R, x2-x>0”的否定是“对?x∈R, x2-x≤0”,即可判断出.
②由p是q的必要不充分条件,可得集合{x|a-1<x≤a}
{x|0<x<2},可得
,解出即可判断出;
③由函数f(x)为幂函数,可得m2-m-1=1,解得m=-1或m=2,代入验证即可得出;
④向量
在向量
方向上的投影是
,计算出即可.
②由p是q的必要不充分条件,可得集合{x|a-1<x≤a}
|
|
③由函数f(x)为幂函数,可得m2-m-1=1,解得m=-1或m=2,代入验证即可得出;
④向量
| a |
| b |
| ||||
|
|
解答:
解:①命题“?x∈R, x2-x>0”的否定是“对?x∈R, x2-x≤0”,故①不正确.
②∵p是q的必要不充分条件,∴集合{x|a-1<x≤a}
{x|0<x<2},∴
⇒1≤a<2.故②不正确.
③∵函数f(x)为幂函数,∴m2-m-1=1,解得m=-1或m=2,当m=-1时f(x)=x-3=
在x=0处没有定义,当m=2时f(x)=x3在x=0处有定义,
∴m=2,故命题③正确;
④向量
在向量
方向上的投影是|
|cos<
=
=
=
,故④错误.
故答案为:③.
②∵p是q的必要不充分条件,∴集合{x|a-1<x≤a}
|
|
③∵函数f(x)为幂函数,∴m2-m-1=1,解得m=-1或m=2,当m=-1时f(x)=x-3=
| 1 |
| x3 |
∴m=2,故命题③正确;
④向量
| a |
| b |
| a |
| a, |
| b> |
| ||||
|
|
| 2 | ||
|
2
| ||
| 5 |
故答案为:③.
点评:本题考查了简易逻辑的判定、函数的性质、向量的投影,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
(
+1)6(
-1)4的展开式中x的系数是( )
| x |
| x |
| A、-3 | B、3 | C、-4 | D、4 |
定义域为R的函数f(x)满足f(x+1)=2f(x),且当x∈(0,1]时,f(x)=x2-x,则当x∈(-1,0]时,f(x)的值域为( )
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
D、[0,
|
已知a>1且实数x,y满足|x|+|y|≤1,则z=ax+y的最大值是( )
| A、1 | ||
| B、a+1 | ||
| C、a | ||
D、
|
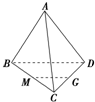
如图所示空间四边形ABCD,连接AC、BD,设M、G分别是BC、CD的中点,则
-
+
等于( )
| MG |
| AB |
| AD |

A、
| ||||
B、3
| ||||
C、3
| ||||
D、2
|