题目内容
2．已知f（x）=2x-1，则f-1（3）=2．分析 根据反函数的性质可知，原函数的值域是反函数的定义域即可求解．
解答 解：f（x）=2x-1，
反函数的性质可知，原函数的值域是反函数的定义域：
即2x-1=3，
可得x=2．
∴f-1（3）=2．
故答案为2．
点评 本题考查了反函数的求法和性质的运用，属于基础题．
练习册系列答案
心算口算巧算一课一练系列答案
应用题作业本系列答案
相关题目
12．我国南北朝时期的伟大科学家祖暅在数学上有突出贡献，他在实践的基础上，于5世纪末提出了下面的体积计算的原理（祖暅原理）：“幂势既同，则积不容异”．“势”是几何体的高，“幂”是截面面积．意思是，若两等高的几何体在同高处截面面积总相等，则这两个几何体的体积相等．现有一旋转体D，它是由抛物线y=x2（x≥0），直线y=4及y轴围成的封闭图形如图1所示绕y轴旋转一周形成的几何体，利用祖暅原理，以长方体的一半为参照体（如图2所示）则旋转体D的体积是（ ）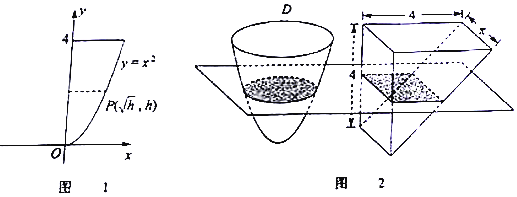
| A． | $\frac{16π}{3}$ | B． | 6π | C． | 8π | D． | 16π |
14．对某地区儿童的身高与体重的一组数据，我们用两种模型①y=bx+a，②y=cedx拟合，得到回归方程分别为${\widehaty^{（1）}}=0.24x-8.81$，${\widehaty^{（2）}}=1.70{e^{0.022x}}$，作残差分析，如表：
（Ⅰ）求表中空格内的值；
（Ⅱ）根据残差比较模型①，②的拟合效果，决定选择哪个模型；
（Ⅲ）残差大于1kg的样本点被认为是异常数据，应剔除，剔除后对（Ⅱ）所选择的模型重新建立回归方程．
（结果保留到小数点后两位）
附：对于一组数据（x1，y1），（x2，y2），…（xn，yn），其回归直线y=bx+a的斜率和截距的最小二乘法估计分别为$\widehatb=\frac{{\sum_{i=1}^n{（{{x_i}-\overline x}）（{{y_i}-\overline y}）}}}{{\sum_{i=1}^n{{{（{{x_i}-\overline x}）}^2}}}}$，$\widehata=\overline y-\widehatb\overline x$．
| 身高x（cm） | 60 | 70 | 80 | 90 | 100 | 110 |
| 体重y（kg） | 6 | 8 | 10 | 14 | 15 | 18 |
| ${\widehate^{（1）}}$ | 0.41 | 0.01 | 1.21 | -0.19 | 0.41 | |
| ${\widehate^{（2）}}$ | -0.36 | 0.07 | 0.12 | 1.69 | -0.34 | -1.12 |
（Ⅱ）根据残差比较模型①，②的拟合效果，决定选择哪个模型；
（Ⅲ）残差大于1kg的样本点被认为是异常数据，应剔除，剔除后对（Ⅱ）所选择的模型重新建立回归方程．
（结果保留到小数点后两位）
附：对于一组数据（x1，y1），（x2，y2），…（xn，yn），其回归直线y=bx+a的斜率和截距的最小二乘法估计分别为$\widehatb=\frac{{\sum_{i=1}^n{（{{x_i}-\overline x}）（{{y_i}-\overline y}）}}}{{\sum_{i=1}^n{{{（{{x_i}-\overline x}）}^2}}}}$，$\widehata=\overline y-\widehatb\overline x$．
12．已知i是虚数单位，若复数z满足z2=-4，则$\frac{1}{z}$=（ ）
| A． | -$\frac{1}{2}$ | B． | -$\frac{1}{2}$i | C． | $±\frac{1}{2}$ | D． | $±\frac{1}{2}$i |