题目内容
 在直三棱柱ABC-A′B′C′中,底面ABC是边长为2的正三角形,D′是棱A′C′的中点,且AA′=2
在直三棱柱ABC-A′B′C′中,底面ABC是边长为2的正三角形,D′是棱A′C′的中点,且AA′=2| 2 |
(Ⅰ)试在棱CC′上确定一点M,使A′M⊥平面AB′D′;
(Ⅱ)当点M在棱CC′中点时,求直线AB′与平面A′BM所成角的大小.
考点:直线与平面所成的角,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)由直三棱柱的性质得到B'D'⊥平面ACC'A',进一步得到B'D'⊥A'M,根据线面垂直的判定定理,只要A'M⊥AD'即可;
(2)建立空间直角坐标系,写出
,
,
的坐标,借助于向量的数量积求线面角的正弦值.
(2)建立空间直角坐标系,写出
| AB′ |
| A′M |
| A′B |
解答:
解:(1)∵直三棱柱ABC-A′B′C′中,底面ABC是边长为2的正三角形,D′是棱A′C′的中点,
∴B'D'⊥A'C',
∴B'D'⊥平面ACC'A',
∴B'D'⊥A'M,
∴在棱CC′上确定一点M,使A′M⊥平面AB′D′,只要过A'作A'M⊥AD'交CC'与点M;
(2)如图建立空间直角坐标系,

因为直三棱柱ABC-A′B′C′中,底面ABC是边长为2的正三角形,D′是棱A′C′的中点,且AA′=2
.
所以A(0,0,0),B'(
,1,2
),A'(0,0,2
),B(
,1,0),
M(0,2,
),
所以
=(
,1,2
),
=(0,2,-
),
=(
,1,-2
),
设平面A'BM的一个法向量为
=(x,y,z),
则
,即
,令y=1,则
=(
,1,
),
cos<
,
>=
=
=
;
所以当点M在棱CC′中点时,直线AB′与平面A′BM所成角的大小为arcsin
.
∴B'D'⊥A'C',
∴B'D'⊥平面ACC'A',
∴B'D'⊥A'M,
∴在棱CC′上确定一点M,使A′M⊥平面AB′D′,只要过A'作A'M⊥AD'交CC'与点M;
(2)如图建立空间直角坐标系,

因为直三棱柱ABC-A′B′C′中,底面ABC是边长为2的正三角形,D′是棱A′C′的中点,且AA′=2
| 2 |
所以A(0,0,0),B'(
| 3 |
| 2 |
| 2 |
| 3 |
M(0,2,
| 2 |
所以
| AB′ |
| 3 |
| 2 |
| A′M |
| 2 |
| A′B |
| 3 |
| 2 |
设平面A'BM的一个法向量为
| n |
则
|
|
| n |
| 3 |
| 2 |
cos<
| n |
| AB′ |
| ||||
|
| 8 | ||||
|
2
| ||
| 3 |
所以当点M在棱CC′中点时,直线AB′与平面A′BM所成角的大小为arcsin
2
| ||
| 3 |
点评:本题考查了正三棱柱的性质以及线面垂直、线面角的求法,关键是正确利用正三棱柱的性质以及借助于空间向量的数量积求线面角的大小,适当建立坐标系,正确写出所需向量的坐标,属于中档题.

练习册系列答案
相关题目
正四棱锥的顶点都在同一球面上,若该棱锥的高为6,底面边长为4,则该球的表面积为( )
A、
| ||
B、
| ||
C、
| ||
| D、16π |
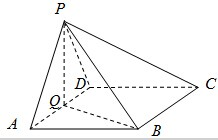 在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,若PA=PD.
在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,若PA=PD.