题目内容
正四棱锥的顶点都在同一球面上，若该棱锥的高为6，底面边长为4，则该球的表面积为（ ）
A、
| ||
B、
| ||
C、
| ||
| D、16π |
考点：球的体积和表面积
专题：球
分析：根据正四棱锥P-ABCD与外接球的关系求出球的半径，即可求出球的表面积．
解答：
解：如图，正四棱锥P-ABCD中，PE为正四棱锥的高，根据球的相关知识可知，正四棱锥的外接球的球心O必在正四棱锥的高线PE所在的直线上，延长PE交球面于一点F，连接AE，AF，
由球的性质可知△PAF为直角三角形且AE⊥PF，
∵底面边长为4，
∴AE=2
，PE=6，
∴侧棱长PA=
=
=
=2
，PF=2R，
根据平面几何中的射影定理可得PA2=PF•PE，
即44=2R×6，解得R=
，
则S=4πR2=4π（
）2=
π，
故选：B
由球的性质可知△PAF为直角三角形且AE⊥PF，
∵底面边长为4，
∴AE=2| 2 |
∴侧棱长PA=
| PE2+AE2 |
62+(2
|
| 44 |
| 11 |
根据平面几何中的射影定理可得PA2=PF•PE，
即44=2R×6，解得R=
| 11 |
| 3 |
则S=4πR2=4π（
| 11 |
| 3 |
| 484 |
| 9 |
故选：B
点评：本题考查球的表面积，球的内接几何体问题，考查计算能力，根据条件求出球的半径是解决本题的关键．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
在直三棱柱ABC-A′B′C′中，底面ABC是边长为2的正三角形，D′是棱A′C′的中点，且AA′=2
在棱长为2的正方体ABCD-A1B1C1D1中，E、F分别为DD1、DB的中点．
已知算法：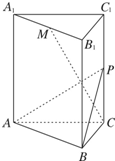
如图，三棱柱ABC-A1B1C1的底面是边长为4正三角形，AA1⊥平面ABC，AA1=2
某市为了了解今年高中毕业生的体能状况，从本市某校高中毕业班中抽取一个班进行铅球测试，成绩在7.95米及以上的为合格．把所得数据进行整理后，分成6组画出频率分布直方图的一部分（如图），已知从左到右前5个小组的频率分别为0.04，0.10，0.14，0.28，0.30，第6小组的频数是7．