题目内容
5.已知点A(5,0),抛物线C:y2=2px(0<p<5)的准线为l,点P在C上,作PH⊥l于H,且|PH|=|PA|,∠APH=120°,则p=( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由抛物线的定义可知:丨PH丨=x1+$\frac{p}{2}$,根据三角形的性质,即可求得P点坐标,代入抛物线方程,即可求得p的值.
解答 解:设P(x1,y1),x1>0,过P点做PD⊥OA,
则由|PH|=|PA|,∠APH=120°,则∠APD=30°,
由抛物线的定义可知:丨PH丨=x1+$\frac{p}{2}$,
∴|PA|=x1+$\frac{p}{2}$,丨AD丨=5-x1,
sin∠APD=$\frac{丨AD丨}{丨AP丨}$,则x1=$\frac{10}{3}$-$\frac{p}{6}$,
则丨PD丨=丨AP丨cos∠APD=$\frac{\sqrt{3}}{2}$($\frac{10}{3}$-$\frac{p}{6}$+$\frac{p}{2}$)=$\frac{\sqrt{3}}{2}$($\frac{10}{3}$+$\frac{p}{3}$),
则P($\frac{10}{3}$-$\frac{p}{6}$,$\frac{\sqrt{3}}{2}$($\frac{10}{3}$+$\frac{p}{3}$),),将P代入抛物线方程,
整理得:p2-12p+20=0,解得:p=2,或p=10(舍去),
∴p的值2,
故选B.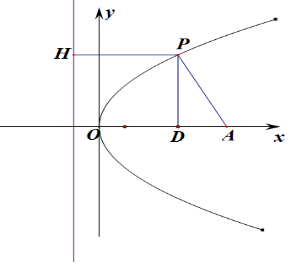
点评 本题考查抛物线的定义及简单几何性质,三角形的性质,考查数形结合思想,属于中档题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
13.若将函数f(x)=cosx-sinx的图象向右平移m个单位后恰好与函数y=-f′(x),的图象重合,则m的值可以为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{3π}{4}$ | D. | π |
10.某几何体的三视图如图所示,则该几何体的表面积为( )


| A. | 8(π+4) | B. | 8(π+8) | C. | 16(π+4) | D. | 16(π+8) |
17.根据下边流程图输出的值是( )


| A. | 11 | B. | 31 | C. | 51 | D. | 79 |