Question

16．在平行四边形ABCD中，E为BC的中点，F在线段DC上，且CF=2DF．若$\overrightarrow{AC}=λ\overrightarrow{AE}+μ\overrightarrow{AF}$，λ，μ均为实数，则λ+μ的值为$\frac{7}{5}$．

Answer 1

分析 设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，则$\overrightarrow{AE}$=$\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$，$\overrightarrow{AF}$=$\frac{1}{3}\overrightarrow{a}$+$\overrightarrow{b}$，从而$\overrightarrow{AC}=\overrightarrow{a}+\overrightarrow{b}$=$λ（\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}）+μ（\frac{1}{3}\overrightarrow{a}+\overrightarrow{b}）$，由此能求出λ+μ．

解答 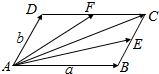解：设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，
∵在平行四边形ABCD中，E为BC的中点，F在线段DC上，且CF=2DF，
∴$\overrightarrow{AE}$=$\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$，$\overrightarrow{AF}$=$\frac{1}{3}\overrightarrow{a}$+$\overrightarrow{b}$，
∵$\overrightarrow{AC}=λ\overrightarrow{AE}+μ\overrightarrow{AF}$，λ，μ均为实数，$\overrightarrow{AC}=\overrightarrow{a}+\overrightarrow{b}$，
∴$\overrightarrow{AC}=\overrightarrow{a}+\overrightarrow{b}$=$λ（\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}）+μ（\frac{1}{3}\overrightarrow{a}+\overrightarrow{b}）$，
∴$\left\{\begin{array}{l}{λ+\frac{μ}{3}=1}\\{\frac{λ}{2}+μ=1}\end{array}\right.$，解得$λ=\frac{4}{5}，μ=\frac{3}{5}$，
∴λ+μ=$\frac{7}{5}$．
故答案为：$\frac{7}{5}$．

点评 本题考查代数式求值，是基础题，解题时要认真审题，注意平面向量加法法则的合理运用．