Question

已知椭圆

x2

4

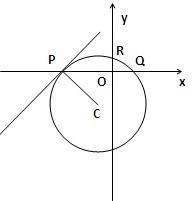
+y2=1，O为坐标原点．若M为椭圆上一点，且在y轴右侧，N为x轴上一点，∠OMN=90°，则点N横坐标的最小值为（　　）

• A、

  2

• B、

  3

• C、2
• D、3

Answer 1

考点：椭圆的简单性质

专题：圆锥曲线中的最值与范围问题

分析：由已知条件，结合椭圆性质，推导出MN的直线方程为y-b=（-

a

b

）（x-a），解得点N的横坐标x=a+

b2

a

，由此利用均值定理能求出点N的横坐标最小值．

解答： 解：椭圆

x2

4

+y2=1，
∵点M（a，b）为椭圆上y轴右侧的点，∴a＞0，
OM的斜率k=

b

a

当点M在顶点（2，0）上时，x轴上不存在点N使得∠OMN=90°
∴k=

a

b

不为0，
∴MN的斜率k=-

1

b a

=-

a

b

，
∴MN的直线方程为y-b=（-

a

b

）（x-a），
令y=0：-b=（-

a

b

）（x-a）
解得点N的横坐标x=a+

b2

a

，
∵

a2

4

+b²=1，b²=1-

a2

4

，
∴x=a+

1- a2 4

a

=a+

1

a

-

a

4

=

3a

4

+

1

a

≥2

3a 4 • 1 a

=

3

．
当且仅当

3a

4

=

1

a

，即a=

2 3

3

时取得最小值

3

，
∴点N的横坐标最小值为

3

．
故选：B．

点评：本题考查点的横坐标的最小值的求法，是中档题，解题时要熟练掌握椭圆的简单性质，要注意均值定理的合理运用．