题目内容
sin4
-cos4
= ．
| π |
| 8 |
| π |
| 8 |
考点：二倍角的余弦,三角函数的化简求值
专题：三角函数的求值
分析：由平方差公式化简后根据同角三角函数关系式及二倍角的余弦公式化简，由特殊角的三角函数值即可得解．
解答：
解：sin4
-cos4
=（sin2
-cos2
）（sin2
+cos2
）=-cos
=-
．
故答案为：-
．
| π |
| 8 |
| π |
| 8 |
| π |
| 8 |
| π |
| 8 |
| π |
| 8 |
| π |
| 8 |
| π |
| 4 |
| ||
| 2 |
故答案为：-
| ||
| 2 |
点评：本题主要考查了平方差公式，同角三角函数关系式，二倍角的余弦公式，特殊角的三角函数值等知识的应用，属于基础题．
练习册系列答案
相关题目
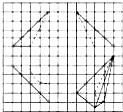如图，网格纸上小正方形的边长为1，粗线或粗虚线画出了某简单组合体的三视图和直观图（斜二测画法），则此简单几何体的体积是
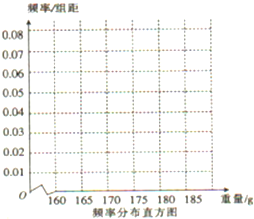云浮市质监部门为迎接2015年春节到来，从市场中随机抽取100个不同生产厂家的某种产品检验质量，按重量（单位；g）分组（重量大的质量高），得到的频率分布表如图所示：