题目内容
下列四个命题:
①对于任意向量
、
,|
-
|≤|
|-|
|;
②向量
,
满足
•
=0,|
|=1,|
|=2,则|2
-
|=2
③对于非零向量
、
,
⊥
的充要条件是:|
+
|=|
-
|;
④在四边形ABCD中,
=2
,则该四边形为等腰梯形.
其中真命题是( )
①对于任意向量
| a |
| b |
| a |
| b |
| a |
| b |
②向量
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| 2 |
③对于非零向量
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
④在四边形ABCD中,
| AD |
| BC |
其中真命题是( )
| A、②③ | B、①③ | C、③④ | D、①④ |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:画图说明命题①④错误;
由已知求出|2
-
|=2
,得到命题②正确;
利用非零向量
⊥
得到等价关系
•
=0,进一步得到等价关系|
+
|=|
-
|,得到命题③正确.
由已知求出|2
| a |
| b |
| 2 |
利用非零向量
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
解答:
解:对于命题①,如图,

令
=
,
=
,则
=
-
,由三角形两边之差小于第三边可知命题①错误;
对于命题②,∵
•
=0,|
|=1,|
|=2,
则|2
-
|=
=
=
=
=2
,命题②正确;
对于命题③,非零向量
⊥
?
•
=0?|
|2+2
•
+|
|2=|
|2-2
•
+|
|2?|
+
|=|
-
|,
∴命题③正确;
对于命题④,如图,
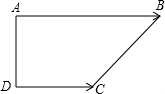
=2
,四边形是梯形,但不一定是等腰梯形,∴命题④错误.
∴正确的命题是②③.
故选:A.

令
| OA |
| a |
| OB |
| b |
| BA |
| a |
| b |
对于命题②,∵
| a |
| b |
| a |
| b |
则|2
| a |
| b |
|2
|
(2
|
4|
|
| 4+4 |
| 2 |
对于命题③,非零向量
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| b |
| a |
| a |
| b |
| b |
| a |
| b |
| a |
| b |
∴命题③正确;
对于命题④,如图,

| AD |
| BC |
∴正确的命题是②③.
故选:A.
点评:本题考查了平面向量的数量积运算,考查了命题的真假判断,体现了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
若a>0,b>0,且lg(a+b)=-1,则
+
的最小值是( )
| 1 |
| a |
| 1 |
| b |
A、
| ||
| B、10 | ||
| C、40 | ||
| D、80 |
设集合M={x|x=k•90°,k∈Z},N={x|x=k•45°+90°,k∈Z},则必有( )
| A、M=N | B、M?N |
| C、M?N | D、M∩N=∅ |
(x-1)6+6(x-1)5+15(x-1)4+20(x-1)3+15(x-1)2+6(x-1)=( )
| A、x6 |
| B、x6+1 |
| C、x6-1 |
| D、(x-1)6-1 |
如果cos(π+A)=-
,那么sin(π+A)=( )
| 1 |
| 2 |
A、-
| ||||
B、
| ||||
C、±
| ||||
D、
|