题目内容
如果cos(π+A)=-
,那么sin(π+A)=( )
| 1 |
| 2 |
A、-
| ||||
B、
| ||||
C、±
| ||||
D、
|
考点:运用诱导公式化简求值,同角三角函数基本关系的运用
专题:三角函数的求值
分析:直接利用诱导公式化简已知表达式,通过A的象限利用同角三角函数的基本关系式,求解即可.
解答:
解:∵cos(π+A)=-cosA=-
,∴cosA=
,
∴sin(π+A)=-sinA,
当为第一象限角时,sinA=
,
当A为第四象限角时,sinA=-
,
∴sin(π+A)=-sinA=±
.
故选:C.
| 1 |
| 2 |
| 1 |
| 2 |
∴sin(π+A)=-sinA,
当为第一象限角时,sinA=
| ||
| 2 |
当A为第四象限角时,sinA=-
| ||
| 2 |
∴sin(π+A)=-sinA=±
| ||
| 2 |
故选:C.
点评:本题考查诱导公式的应用,同角三角函数的基本关系式,考查分类讨论思想以及计算能力.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
若命题“?x0∈R,x02-3mx0+9<0”为真命题,则实数m的取值范围是( )
| A、[-2,2] |
| B、(-2,2) |
| C、(-∞,-2]∪[2,+∞) |
| D、(-∞,-2)∪(2,+∞) |
下列四个命题:
①对于任意向量
、
,|
-
|≤|
|-|
|;
②向量
,
满足
•
=0,|
|=1,|
|=2,则|2
-
|=2
③对于非零向量
、
,
⊥
的充要条件是:|
+
|=|
-
|;
④在四边形ABCD中,
=2
,则该四边形为等腰梯形.
其中真命题是( )
①对于任意向量
| a |
| b |
| a |
| b |
| a |
| b |
②向量
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| 2 |
③对于非零向量
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
④在四边形ABCD中,
| AD |
| BC |
其中真命题是( )
| A、②③ | B、①③ | C、③④ | D、①④ |
停车场一排12个车位,停8辆车,空位连在一起的概率为( )
A、
| ||
B、
| ||
C、
| ||
| D、以上都不对 |
运行如图程序,如果输入x=
,则输出结果y为( )

| π |
| 6 |

A、2
| ||
| B、3 | ||
| C、2 | ||
D、
|
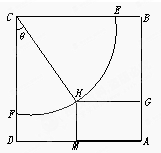 某体育馆拟用运动场的边角地建一个矩形的健身室(如图所示),ABCD是一块边长为50m的正方形地皮,扇形CEF是运动场的一部分,其半径为40m,矩形AGHM就是拟建的健身室,其中G、M分别在AB和AD上,设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在何处时,该健身室的面积最大,最大面积是多少?
某体育馆拟用运动场的边角地建一个矩形的健身室(如图所示),ABCD是一块边长为50m的正方形地皮,扇形CEF是运动场的一部分,其半径为40m,矩形AGHM就是拟建的健身室,其中G、M分别在AB和AD上,设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在何处时,该健身室的面积最大,最大面积是多少?